Показатели надежности восстанавливаемых систем в процессе применения.
Существует два типа систем:
1) системы, которые допускают незначительные перерывы в своей работе.
2) системы, которые не допускают перерывов в своей работе.
Для второго типа систем предусматривается избыточность аппаратуры, и при выходе из строя какого-либо устройства происходит либо замена какого-либо устройства на резервное, либо реконфигурация системы. Для такого рода систем чрезвычайно важное значение имеет свойство готовности (способность находиться в процессе эксплуатации значительную долю времени в работоспособном и готовом к применению состоянии).
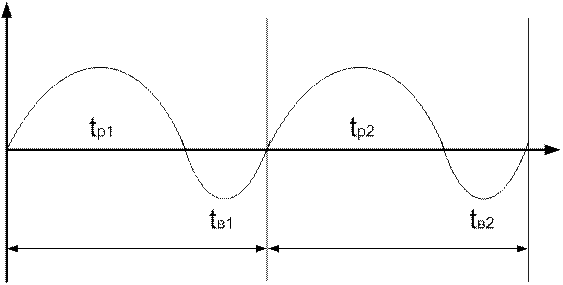
рис. 1
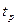 - время работы
- время работы
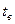 - время восстановления
- время восстановления
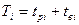 - i-й цикл (1)
- i-й цикл (1) 
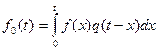 (2)
(2)
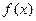 – плотность распределения времени безотказной работы;
– плотность распределения времени безотказной работы;
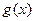 – плотность распределения времени восстановления объекта;
– плотность распределения времени восстановления объекта;
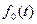 – плотность распределения между очередными отказами.
– плотность распределения между очередными отказами.
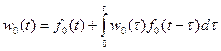 (3)
(3)
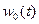 - параметр функции (1)
- параметр функции (1)
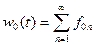
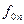 - плотность распределения n-го восстановления.
- плотность распределения n-го восстановления.
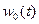 - параметр потока отказа.
- параметр потока отказа.
Другой важнейший параметр – вероятность застать систему в работоспособном состоянии – Г(t).
Г(t) + П(t) = 1
где П (t) – функция неготовности.
Объект может находиться в момент t в работоспособном состоянии при осуществлении одного из двух несовместных событий:
1) объект в течение времени от 0 до t не отказал;
2) объект отказывал и восстанавливался, потом мог опять отказать и восстановиться, и к моменту времени t объект больше не отказывал.
Функция готовности Г(t) равна сумме вероятностей указанных событий.
Вероятность первого события: ????????????????????????????????12
Для определения вероятности 2-го события рассмотрим малый интервал времени 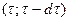 , имея в виду, что данному интервалу предшествует время работы. Тогда вероятность того, что на этом малом интервале закончится ??????????? n-ое восстановление и объект больше не откажет ?????????????, равно:
, имея в виду, что данному интервалу предшествует время работы. Тогда вероятность того, что на этом малом интервале закончится ??????????? n-ое восстановление и объект больше не откажет ?????????????, равно:
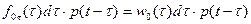
Проигнорировав выражение от 0 до t, получим конечное выражение:
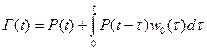
Г(t) – функция готовности.
Согласно узловой теореме теории восстановления:
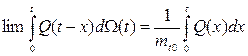
где 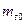 - математическое ожидание времени между очередными событиями;
- математическое ожидание времени между очередными событиями;
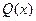 - возрастающая функция на интервале
- возрастающая функция на интервале 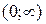 ????????????????????
????????????????????
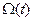 -математическое ожидание числа отказов на интервале
-математическое ожидание числа отказов на интервале 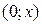 ???????????????
???????????????

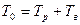
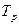 - среднее время работы
- среднее время работы
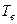 - среднее время восстановления
- среднее время восстановления
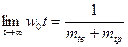
Тогда:
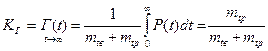
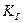 - коэффициент готовности.
- коэффициент готовности.
Но коэффициент готовности недостаточен для характеристики надежности всей системы, так как эта величина относительная.. Нужны еще дополнительные характеристики (которые могут дать реальные интервалы действия и времени).
Таким образом, функция готовности в пределе (при 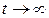 ) переходит в коэффициент готовности, а коэффициент готовности не зависит уже от функции распределения времени наработки на отказ и функции распределения времени восстановления.
) переходит в коэффициент готовности, а коэффициент готовности не зависит уже от функции распределения времени наработки на отказ и функции распределения времени восстановления.
По ГОСТ коэффициент готовности определяется как вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта не предусмотрено.
Коэффициент готовности можно понимать как долю времени, в течение которого объект работоспособен, к общему времени эксплуатации.
При фиксированных значениях 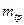 и
и 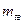 стационарный режим наступает тем медленнее, чем меньше дисперсия случайной величины T0. Очень часто используется коэффициент готовности за период эксплуатации:
стационарный режим наступает тем медленнее, чем меньше дисперсия случайной величины T0. Очень часто используется коэффициент готовности за период эксплуатации:
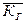
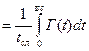
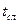 - время службы (всего срока службы)
- время службы (всего срока службы)
Если считать, что функция распределения экспоненциальная, то тогда:
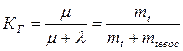
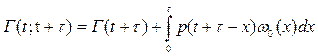
Функция готовности Густ (устанвившаяся):
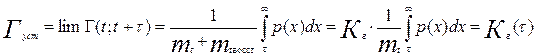
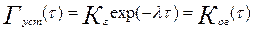
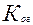 - коэффициент оперативной готовности
- коэффициент оперативной готовности
 При допущении экспоненциальности законов распределения процесс изменения состояния объекта будет марковским с непрерывным временем и конечным множеством состояний. Определим вероятность того, что объект окажется работоспособным в момент времени
При допущении экспоненциальности законов распределения процесс изменения состояния объекта будет марковским с непрерывным временем и конечным множеством состояний. Определим вероятность того, что объект окажется работоспособным в момент времени 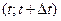 . Обозначим нахождение объекта в работоспособном состоянии в момент времени t как P(t) (не путать с P(t) – вероятностью безотказной работы на интервале
. Обозначим нахождение объекта в работоспособном состоянии в момент времени t как P(t) (не путать с P(t) – вероятностью безотказной работы на интервале 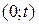 ).
).
Объект может находиться в работоспособном состоянии при следующих несовместимых событиях:
1) работоспособный объект к моменту времени t останется работоспособным в течение времени 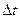 .
.
2) неработоспособный объект к моменту времени t будет за время 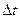 восстановлен.
восстановлен.
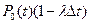
Вероятность того, что к моменту 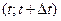 объект будет в работоспособном состоянии.
объект будет в работоспособном состоянии.
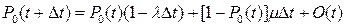
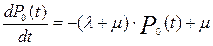
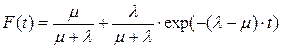 ?????????????????????????
?????????????????????????
| <== предыдущая лекция | | | следующая лекция ==> |
| Характеристики надежности, определяемые с помощью моделей ТМО | | | ОПРЕДЕЛЕНИЕ РЕГРЕССИИ |
Дата добавления: 2016-08-07; просмотров: 743;
