ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ

На линии контакта двух несмешивающихся жидкостей и газа (рис.3) или жидкостей с твердыми телами и газами (рис.4) обнаруживаются молекулярные явления, которые приводят к понятиям смачивания и несмачивания.

Капля более лёгкой жидкости 2, пущенная на поверхность жидкости 1, принимает форму линзы. К единице длины линии контакта жидкость-1 – жидкость-2 – газ будут приложены три силы численно равные коэффициентам поверхностного натяжения: α₁₂ – по границе жидкость-1- жидкость-2; α₂₃ – по границе газ – жидкость-2; α₁₃ – по границе жидкость-1- газ. Силы α₁₂ и α₂₃ стремятся стянуть каплю 2 в сферу, а сила α₁₃ , наоборот, растянуть каплю по поверхности жидкости 1. Если α₁₃ > α₂₃ + α₁₂, то капля 2 неограниченно растекается по поверхности жидкости 1. Имеет место смачивание жидкости 1 жидкостью 2. Аналогичная ситуация будет иметь место на границе жидкость-твёрдое тело-газ (рис.4). Явления такого рода получили название краевых эффектов. Критерием этих состояний является так называемый краевой угол θ. Вершина угла θ лежит в точке на линии контакта всех трёх сред, а лучами являются касательные к поверхностям контактирующих тела. Если краевой угол θ острый, то имеет место смачивание. При тупом угле θ – несмачивание. Полное смачивание при θ = 0⁰, несмачивание при θ = 180⁰.

Явление смачивание-несмачивание приводит к искривлению формы свободной поверхности жидкостей около стенок сосудов. Всякая искривленная поверхность обуславливает дополнительное давление на жидкость со стороны поверхностного слоя в силу его стремления к сокращению.

Первым на это обратил внимание Лаплас, который установил, что дополнительное давление поверхностного слоя на жидкость

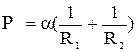, (8)

где R₁ и R₂ радиусы кривизны поверхности в двух её любых взаимно перпендикулярных, нормальных сечениях.

Для сферической поверхности, это дает

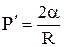. (9)

Для цилиндрической –

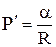. (10)

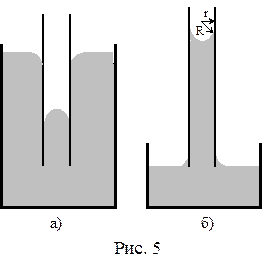
Лапласовское давление объясняет широкий круг капиллярных явлений. Эффект искривления поверхности жидкости у стенок особенно заметен в сосудах малого диаметра (трубка, щель). Если жидкость не смачивает стенки капиллярного сосуда, то форма поверхности (мениск) будет выпуклой (рис.5а), если смачивает, то вогнутой (рис.5б).

Из рисунка видно, что для вогнутого мениска давление в жидкости будет снижаться (рис.5б), а для выпуклого увеличиваться (рис.5а) по сравнению со случаем плоской поверхности. Высота поднятия (опускания) жидкости в капилляре по сравнению с уровнем жидкости в широком сосуде определяется законом Борелли-Жюрена:

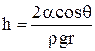. (11)

Методы определения коэффициента поверхностного натяжения: метод капель, метод отрыва кольца, капиллярный метод, метод Ребиндера и др.

ТВЕРДЫЕ ТЕЛА.

Твердое тело – агрегатное состояние вещества, для которого характерно наличие значительных сил межмолекулярного взаимодействия, стабильность формы и объема. Тепловое движение частиц твердого тела представляет собой небольшие по амплитуде колебания около положений равновесия. Различают кристаллическое и аморфное строение твердых тел.