Если прямая не параллельна плоскости, то она пересекает ее под тем или иным углом.

Задача на пересечение прямой с плоскостью является одной из основных задач.

Алгоритм или план решения таких задач будет следующий.

1) Заключаем отрезок прямой во вспомогательную проецирующую плоскость и находим линию пересечения плоскостей.

2) Находим точку пересечения отрезка прямой с линией пересечения плоскостей, которая будет искомой точкой пересечения прямой с заданной плоскостью.

3) Определяем видимость отрезка прямой используя метод конкурирующих точек.

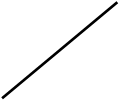
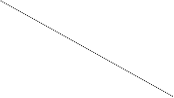
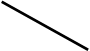
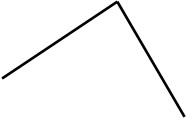
Например. Отрезок DE общего положения пересекает плоскость общего положения АВС .

T2 D2 B2

3 2 12

K 2

A2 22 C2

42

E2

E1

11 B1

K1

A 1

D1 31º 41 21 C1

Заключаем отрезок DE во фронтально проецирующую плоскость Т .

Находим проекции линии пересечения 1,2, сначала фронтальную проекцию 12, 22 , а затем горизонтальную 11,21. Находим горизонтальную проекцию точки К1, а затем фронтальную К2.

Для определения видимости воспользуемся конкурирующими точками 3 и 4.

На горизонтальной проекции точка 31 принадлежащая прямой накладывается на точку 41 принадлежащую плоскости, однако достаточно по линии проекционной связи подняться на фронтальную плоскость проекций и видим, что точка 32 выше точки 42. Значит до точки пересечения с плоскостью прямая на горизонтальной проекции видима.

Примените самостоятельно этот метод для определения видимости фронтальной проекции прямой.