Где Н —• высота Наводного борта, м 2 страница
Угол tf измеряется от линии ветра в сторону, противоположную стороне перекладки руля, до линии, соединяющей точки 2 и 3. Дистанции циркуляции 5 — расстояние между этими точками. Угол зависит в общем случае от целого ряда параметров судна, характеризующих его гидродинамические и аэродинамические особенности. Значения угла if и дистанции S могут быть рассчитаны с помощью ЭВМ, поскольку требуется решение системы дифференциальных уравнений. Наличие в уравнениях большого числа коэффициентов, значения ко- юрых определяются приблизительно, ограничивает возможности расчетных методов циркуляции в условиях ветра п волнения.
На рис 11.3 приведены результаты расчета циркуляции в условиях ветра и волнения для теплохода «Борис Бувин» в балласте. Стрелками показано направление ветра. Сравнение расчетных траекторий с широкомасштабными натурными данными показало, что точность paj* работанного на кафедре управления судном ЛВИМУ им. адм. С О. Макарова экспериментально-расчетного метода определения циркуляции в условиях ветра и волнения лежит в пределах 17—19 % при опре-


делении тактического диаметра циркуляции и 10 % в определении выдвига
В обязательной информации в таблице маневренных элементов управляемость судна представлена лишь поворотливостью. С практической точки зрения, в реальных условиях плавания не менее важное значение имеет оценка судоводителями возможности осуществления прямолинейного движения судна в условиях ветра. Судоводитель дол* жен располагать информацией, позволяющей ему судить о возможности осуществления управляемого движения в определенном направлении относительно курсового угла ветра как на глубокой воде, так и на мелководье, об углах дрейфа, с которыми это движение осуще-^ ствляется.
Инерционно-тормозные характеристики. Влияние ветра на инер- ционно-тормозные характеристики во многом зависит от конструктивных особенностей судна, однако для встречного ветра (<?=0°) и попутного (<7=180°) можно проследить некоторые особенности этого влияния. В первую очередь представляет интерес ветер силой 8 м/с (4 балла) — предельно допустимый при сдаточных испытаниях. Результаты моделирования свободного и активного торможения среднестатистических судов морского флота, смоделированные по средним параметрам 25 типов судов, показывают, что у судов водоизмещением более 10 тыс. т инерционно-тормозные характеристики при ветре до 4 баллов включительно могут отличаться друг от друга до 26 % п выбегу и до 8 % по тормозному пути. Отличия от штилевых значений- составят 18 % по выбегу и 4 % по тормозному пути. Под выбегом суд* на при свободном торможении здесь понимается путь, пройденный от начала свободного торможения до достижения 20 % начальной скорости.
Учитывая значительную величину погрешностей, результаты на турных испытаний, проведенные при ветре, должны быть исправлень и приведены к условиям безветрия. Если влияние ветра на активно' торможение может быть скомпенсировано повторением эксперимента! на обратном курсе и осреднением, то для свободного торможения маневрирование на прямом и обратном курсе и осреднение не обеспечи-о вают компенсации сноса даже при курсовых углах ветра 0 и 180°. Од нако можно ограничиться одним экспериментом, проведенным пр встречном или попутном ветре, если каждое экспериментальное значение S*(V) для приведения к безветрию умножить на поправочный коэффициент ц (рис. N.4), зависящий от скорости ветра и отношения фактической скорости в каждый момент замера к начальной скорости.
Влияние ветра на инерционно-тормозные характеристики усиливается на промежуточных курсовых углах ветра. На рис. 11.5 показана влияние курсового угла ветра скоростью 8 м/с на параметры свободного торможения теплохода «Борис Бувин». Пунктиром показано значение выбега судна при безветрии. Вследствие первоначального движения с углом дрейфа при свободном торможении судно начинает терять управляемость и приводится к ветру. Максимальный угол отклонения от курса 85,5° и максимальное боковое отклонение 0,77 кб происходят при курсовых углах ветра 100—130°, однако наиболее быстро судно тормозится при начальных курсовых углах ветра 40—60Р. Аналогичная информация может быть получена для любого типа судов морского флота после моделирования его движения.
Влияние ветра и волнения. На рис. 11.6 приведено сопоставление расчетной и экспериментальной траекторий теплохода «Борис Бувин»
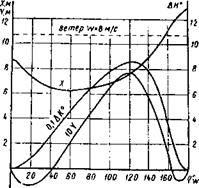 Рис. 11.5. Параметры свободного торможения теплохода «Борис Бувин»:
X — смещение в направлении линии первоначального курса; Y — смещение в направлении перпендикулярной липни первоначального курса; ДК° — угол изменения курса вправо к кон. ну свободного торможения (V”0,2V*)
Рис. 11.5. Параметры свободного торможения теплохода «Борис Бувин»:
X — смещение в направлении линии первоначального курса; Y — смещение в направлении перпендикулярной липни первоначального курса; ДК° — угол изменения курса вправо к кон. ну свободного торможения (V”0,2V*)
|

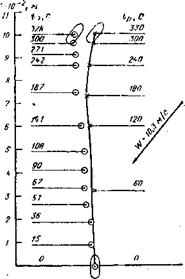 Рис. 11.6. Сопоставление расчетной и экспериментальной траектории движении теплохода «Борис Бувин» при маневре ППХ—СТОП; h, ip — экспериментальное и расчетное время соответствующей позиции; ветер 10,3 м/с; волнение 2 м
Рис. 11.6. Сопоставление расчетной и экспериментальной траектории движении теплохода «Борис Бувин» при маневре ППХ—СТОП; h, ip — экспериментальное и расчетное время соответствующей позиции; ветер 10,3 м/с; волнение 2 м
|

при маневре «ППХ—СТОП» при ветре скор стью 10,3 м/с и волнении h—2 м. Приведе ные на рис. 11.6 данные дают основание г ворить о хорошей сходимости результатов пригодности алгоритма для анализа измен ния инерционно-тормозных характерист конкретных типов судов в условиях ветрово нового воздействия.
 Дополнительное уменьшение выбега тормозного пути судна вследствие вол пени значительно. Однако до Лз% «l-f-1,5 м суще?; ственного влияния волнения не отмечается.
Дополнительное уменьшение выбега тормозного пути судна вследствие вол пени значительно. Однако до Лз% «l-f-1,5 м суще?; ственного влияния волнения не отмечается.
Ветроволновое воздействие на инерцион но-тормозные характеристики носит индив Р„С 118 Экстренное юрмо- дуальный характер для каждого типа суди жение теплохода «Борис При этом может учитываться либо среднеста Бувин» в зависимости от тистическое волнение, сответствующее каждо неврГппх” ПЗХ* ЛЛЯ МЭ скорости ветра, либо с конкретными значения-
ви высот волн 3%-ной обеспеченности и коэффициентами развитости волнения.
Информация о ветроволновом влиянии может носить обобщенный» характер (рис. 11.7) или быть представлена в виде конкретных траекторий (рис. 11.8).
Ориентировочные оценки точности применяемости метода: по ак тивиому торможению 65т^14%; б/т^20 %; по свободному торможению aSt^9 %; 6S(V)^17 % (в конце свободного торможения). Па? сбавлению хода 65(0^8% разгону 6S(V)^14%. Обобщая, можно сказать, что расстояние, пройденное судном до достижения определенной скорости V, получено с погрешностью, не превышающей 18 % при свободном торможении и подтормаживании и 15 % при активном торможении и разгоне.
11.4. Обоснование выбора курса и скорости при плавании на волнении
Судно, отклоненное от положения устойчивого равновесия на ти-< хой воде и затем предоставленное самому себе, будет совершать колебания относительно положения равновесия, называемые собственными или свободными. Они возникают при вертикальной, бортовой и килевой качке.
Колебания, вызываемые волнением, называются вынужденными. Эти колебания возникают при всех видах качки (в том числе при продольной горизонтальной, поперечно-горизонтальной, а также при рыскании судна).
На регулярном волнении свободные колебания очень быстро затухают и остаются только вынужденные.
При равенстве значений периода собственных колебаний и периода возмущающей апы наблюдается резкое увеличение амплитуд, называемое резонансом соответсгвущего вида качки. Резонанс может иметь место только при вертикальной, бортовой и килевой качке. На рис. 11.9 в качестве примера приведен характерный график зависимости амплитуды 0О бортовой качки на регулярном волнении от отношения периода собственных колебаний судна 7® к периоду возмущающей силы т.
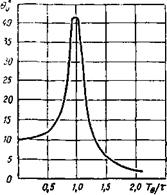 Рис 11.9. Типичная амплитудно-ча- стотная характеристика бортовой качки судна
Рис 11.9. Типичная амплитудно-ча- стотная характеристика бортовой качки судна
|


 При нерезонансных режимах бортовой качки на регулярном волнении ее амплитуды будут определяться формулой
При нерезонансных режимах бортовой качки на регулярном волнении ее амплитуды будут определяться формулой

 (112)
(112)
Ть
где по...... наибольший уклон взволнованной поверхности.
Как следует из формулы (И.2):
 0о<1,95ао при {Те/х)С0,7; при (7*0ут)]>1
0о<1,95ао при {Те/х)С0,7; при (7*0ут)]>1
Угол ао обычно не превышает 8—10°, причем его величина уменьшается с ростом длины волны. Поэтому, если курс и скорость на волнении будут подобраны таким образом, что на регулярном волнении отношение Т%(х будет меньше 0,7, то амплитуда бортовой качки в
этом случае не будет превышать 20°, а при 7*в/, >1,3—15°. Наложение в последнем случае более жестких ограничений на предельные значения амплитуд связано с тем, что при T$fx >*1,3 следует ожидать неблагоприятных значений угла сдвига фаз колебаний судна по отношению к волнам.
Кажущийся период волны
 1,95 Я,
1,95 Я,
с+у cos q
При неограниченно больших отношениях глубины к длине судна формула (10.3) приобретает вид
(П.Ь)
19£
| Л/а* | Отношение высоты борта к .ширине судна Н/В | |||||
| 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0,8 | |
| 0,9 | 0,62 | 0,64 | 0,66 | 0,69 | 0,73 | 0,76 |
| 1 ,о | 0,65 | 0,67 | 0,69 | 0,72 | 0,76 | 0,79 |
| 1,1 | 0,68 | 0,70 | 0,72 | 0,75 | 0,78 | 0,82 |
| 1,2 | 0,71 | 0.73 | 0,75 | 0,78 | 0,81 | 0,84 |
| 1 ,з | 0,74 | 0,76 | 0,78 | 0,82 | 0,83 | 0,86 |
| 1,4 | 0,76 | 0,78 | 0,80 | 0,82 | 0,85 | 0,88 |
| 1,5 | 0,78 | 0,80 | 0,82 | 0,84 | 0,87 | 0,90 |
| 1,6 | 0,81 | 0,82 | 0,84 | 0,87 | 0,89 | 0,92 |
| 1,7 | 0,83 | 0,85 | 0,87 | 0,89 | 0,92 | 0,94 |
| 1,8 | 0,85 | 0,87 | 0,89 | 0,92 | 0,94 | 0,96 |
| 1,9 | 0,88 | 0,90 | 0,92 | 0,94 | 0,96 | 0,98 |
| 2,0 | 0,90 | 0.92 | 0,94 | 0,96 | 0,98 | 1,00 |
| Примечание, б — коэффициент общей полноты корпуса судна; а— коэффициент полноты ватерлинии. |
Таким образом, изменяя курс или скорость судна, можно изменять значения кажущегося периода волны т и избежать резонанса или резонансной зоны, определяемой зависимостью,
 0,7<-
0,7<-
или, что то же самое,
|  |
|
Для расчетного определения периодов собственных бортовых колебаний может быть использована формула
Гв=—, (ИЛ)
где — коэффициент, зависящий от типа судна и состояния нагрузки;
В — ширина судна;
А — начальная поперечная метацентрическая высота.
ИМО рекомендует принимать следующие приближенные значения коэффициента k% для каботажных и промысловых судов.
Суда каботажного плавания (кроме танкеров) в балласте — 0,88; промысловые суда с полными запасами для открытого моря — 0,80; креветочные прибрежного лова 0,95; с танками для живой рыбы — 0,60.
Приближенные значения коэффициента k% для морских транспортных судов в грузу (кроме танкеров и газовозов) приведены в табл. 11.3
Значения периода собственных продольных колебаний дает график, представленный на рис. 11.10.
Исследования, проведенные Ю. В. Ремезом, показали, что разработанная им униБерсальная штормовая диаграмма может быть с достаточной для практики точностью использована как при регулярном, так и нерегулярном волнении. Входя в диаграмму по среднему кажущемуся периоду, можно успешно определять сочетания курсов и скоростей, отвечающих резонансным режимам бортовой и килевой качки на реальном морском волнении.
11.5. Универсальные штормовые диаграммы Ю. В. Ремеза
Для облегчения задачи управления судном в шторм советскими учеными были предложены специальные диаграммы для выбора курса и скорости в штормовых условиях. Такие диаграммы разработаны В. Г. Власовым, С. Н. Благовещенским, Л. М. Ногидом, Ю. В. Ремезом.
В практике плавания наибольшее распространение получили универсальные диаграммы Ю. В. Ремеза для больших и произвольных глубин.
В теории волн глубина считается большой, если она превышает половину длины волны. Однако для целей практики применение универсальной штормовой диаграммы Ю. В. Ремеза для больших глубин можно расширить до значений глубин, превышающих четверть длины волны. Это будет соответствовать общей точности исходных данных.
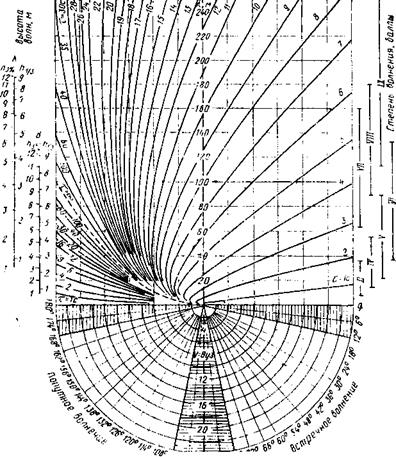
Универсальная диаграмма для больших глубин (рис. 11.11) состоит из верхней и нижней частей.
По вертикальной оси верхней части диаграммы отложены длины волн X, по горизонтальной — проекции скорости судна на линию бега волн Vcos^. Здесь V — скорость судна, уз; q — курсовой угол бега волн, град.
Правая половина диаграммы отвечает ходу на встречном волнении, под которым понимаются курсы прямо против волны (вразрез волне) и волна в скулу. Средняя вертикаль соответствует курсу лагом к волне при любой скорости судна либо любому положению судна по отношению к набегающим волнам при нулевой скорости. Левая половина отвечает ходу на попутном волнении, включая в это понятие курсы волны в раковину и прямо по волне. Левой половине диаграммы соответствуют отрицательные значения Vcosq(§(f<q<. 180°).
Верхняя часть диаграммы содержит семейство кривых, каждая из которых построена для определенного значения кажущегося периода волны т. Эти значения надписаны на соответствующих кривых.
Когда судно не имеет хода либо идет лагом к волнам, кажущийся период волны т совпадает с ее истинным периодом (периодом по отношению к неподвижному наблюдателю) т0. Таким образом, ордината пересечения вертикальной оси диаграммы с кривой, отвечающей данному значению кажущегося периода т, определяет собой длину волны А,, истинный период которой равен то. Так, например, при то= =8с т=100 м, при то=12с Х — 225 м и т. д. На встречном волнении кажущийся период волны оказывается меньше истинного, на попутном, если только судно не обгоняет волну, — больше истинного.
Если на попутном волнении проекция скорости судна на направление распространения волн Vcos</ совпадает со скоростью волн, которая равна 2,43 \ПГ уз, то кажущийся период волны обращается в бесконечность, т. е. волны на судно не набегают и он$ движется, как бы «оседлав» волну. В этом случае на чисто попутном волнении судно по отношению к системе волн как бы неподвижно. Наблюдателю, находящемуся на судне, будет казаться, что оно дрейфует.
Указанному случаю на диаграмме соответствует штриховая кривая х = оо.
Нижняя часть диаграммы включает семейство концентрических полуокружностей с центром, расположенным в начале координат диаграммы, и пучок лучей, исходящих из центра. Каждая полуокружность отвечает определенному значению скорости V (уз), каждый луч — определенному курсовому углу q. Правая часть диаграммы отвечает встречному, а левая — попутному волнению.
Поскольку при построении диаграммы принято, что волны бегут справа налево, вектор скорости судна направлен из центра к периферии ее нижней части вдоль луча, соответствующего данному значению курсового угла q. Определенному сочетанию скорости судна и курсового угла отвечает точка нижней части диаграммы, являющаяся конном вектора скорости судна.
| 21 20 19 18 | 16 15 П | U | 12 11 10 У 3 ? | 6 5 4 | rdU5 | |
| Г"( • Т-.' -Г— 1 —1—1—1—г 1 f 1 1 1 1 1 III- | г~т • 1 i | ■*T | :—!—ГТ' т T I ! 1 i ' > 1 . 1 l 1 1 1 i 1 i 1 1 1 ! 1 1 1 | 1 i.li. l li i | | J | |
| 28 27 26 25 2k 2) 22 | Zi 20 19 id | r> | 16 15 П 13 13 // 10 9 | 3 7 6 5 | *, T*'c | |
| <t0 38 36 J4 | 30 28 26 | 2b | 22 20 18 16 П | 12 10 8 | STc/0,7 |
 7102°9бо до0 6Ь° 7йР ^
Рис. ПН. Универсальная шгормоная диаграмма Ю. В Ремеза для больших глубин: Кдлина волны.Vckopocn суд.ы. d курсовой угол бега волны
7102°9бо до0 6Ь° 7йР ^
Рис. ПН. Универсальная шгормоная диаграмма Ю. В Ремеза для больших глубин: Кдлина волны.Vckopocn суд.ы. d курсовой угол бега волны
|
Нижняя часть диаграммы дает возможность графически находить значения Kcos^ при данном сочетании V и q, а также решать обратную задачу определения всех значений V и q, отвечающих заданной величине К cos q.
Так, например, если У=12 уз, а ^=609, то, проводя через точку пересечения соответствующих окружностей и луча вертикальную прямую, найдем по пересечению последней с горизонтальной осью диаграммы, что У cos <7=6 уз.
Решение обратной задачи сводится к проведению из нижней части диаграммы вертикальной прямой, абсцисса которой представляет собой заданную величину V cos q. Указанная задача имеет бесчисленное множество решений, так как для всех точек, лежащих на этой прямой, значения Vcosq> для которых конец вектора скорости судна располагается на указанной вертикальной прямой, являются решением поставленной задачи.
Например. Проводя на нижней части диаграммы вертикальную прямую, соответствующую Vcos<7 = 8y3: при q~*Q° V—8 уз; при q — 45° У=11,5 уз; при (/=60° У-16 уз и т. д.
Зоны курсовых углов, близких к нулю или 180°, когда бортовая качка оказывается незначительной даже в условиях резонанса, но можно ожидать усиления килевой качки, отмечены на графике вертикальной штриховкой. Зона курсовых углов, близких к 90°, когда судно располагается почти лагом к волне и резонанс бортовой качки становится особенно опасным, а килевая оказывается весьма малой, отмечена горизонтальной штриховкой.
Над диаграммой помещена вспомогательная шкала для определения значений т, ограничивающих резонансные зоны качки. Иа средней линии этой шкалы нанесены величины периода собственьыл колеба ний судна Ть а на верхней и нижней линиях на тех же вертикалях отложены Ге/1,3 и Т9 /0,7 соответственно.
На шкалах Ли В, расположенных слева от диаграммы, ь*ие:евы высоты нерегулярных волн 3 %-ной обеспеченности и значительного волнения Л1/3- Справа от диаграммы помещена шкала степени волне- пни в баллах.
Таким образом, диаграмма допускает три входа: по длине волны, по высоте волны и по степени волнения.
Как уже указывалось, приведенная универсальная штормовая диаграмма применима с достаточной точностью для глубин, превышающих четверть длины судна. Резонансная качка на волнах повышенной крутизны, характерных для мелководья, особенно опасна для небольших судов. В связи с этим Ю. В. Ремезом разработана универсальная штормовая диаграмма, позволяющая оперативно выбирать безопасные курсы и скорости судна при шторме на любых, в том .числе и на весьма малых глубинах. «
1.
11.6. Использование универсальной штормовой диаграммы
Из трех возможных входов в диаграмму (по длине волны, по высоте волны и по степени волнения в баллах) при непосредственном выборе безопасных курсов и скоростей судна, находящегося в штормовой обстановке, следует использовать вход по длине волны.
Для определения границ резонансных зон на диаграмме проводятся вертикальные прямые через точки пересечения горизонтальной
линии, отвечающей данной длине волны А, с кривыми т=Тя /0,7 и т=7'в/1,3.
Вертикальные линии, точно соответствующие резонансу, являются осями симметрии соответствующих резонансных зон. Иными словами, горизонтальные расстояния от этих линий до линий, отвечающих правой и левой границам резонансных зон, одинаковы. Это свойство можно использовать для контроля правильности определения границ резонансных зон.
Пример 1. Определить резонансные сочетания курсовых углов н скоростей и границы резонансных зон бортовой качки для судна, имеющего период собственных колебаний Т9 = 12 с на волне длиной Л=30 м.
Решение (рис. 11.12). Находим точки С и D пересечения горизонтальной прямой Х = 30 м с кривыми т=Т 9 «*12 с. Проводим через эти точки вертикальные линии, определяющие сочетания курсовых углов и скоростей, точно отвечающих резонансу.
По вспомогательной шкале, помещенной над диаграммой, прочитываем значения т, соответствующие границам зон. При «* 12 с они приближенно равны 9,2 и 17,2 с.
Далее следует найти на диаграмме точки Сх и С2 пересечения горизонтальной прямой Х=30 м с кривыми т=9,2 с и т = 17,2 с глазомерной интерполяцией. Через точки проводим вертикальные прямые, определяющие границы резонансных зон. Эти зоны на рис. 11.12 заштрихованы.



 Для избежания усиленной бортовой качки в режиме резонанса или близких к нему режимах следует выбрать скорость и курс судна относительно волн так, чтобы вектор скорости судна оканчивался вне зашрихован- ных зон.
Для избежания усиленной бортовой качки в режиме резонанса или близких к нему режимах следует выбрать скорость и курс судна относительно волн так, чтобы вектор скорости судна оканчивался вне зашрихован- ных зон.
Резонанс бортовой качки не приводит к существенному росту амплитуд на чисто встречном или чисто попутном волнении и близких к ним курсах. Секторы, соответствующие таким курсовым углам (0—12°, 168—180°), на диаграмме заштрихованы вертикальной штриховкой. На рис. 11.12 эти секторы не показаны.
Таким образом, если конец вектора скорости судна попадет в верхние части резонансных зон, которые оставлены незаштрихо- ванными, то режим бортовой качки не должен считаться опасным.
Опасность, наоборот, возрастет, если вектор скорости оканчивается в нижних частях резонансных зон бортовой качки, т. е. курсовой угол приближается к 90°. Безоговорочно должны исключаться такие сочетания курсов и скоростей, при которых конец вектора скорости судна
принадлежит резонансной зоне бортовой качки, а курсовой угол волны заключен в пределах 78°<<7<102°.
Примнр 2. Определить резонансные сочетания курсовых углов и скоростей и границы резонансной килевой качки для судна, имеющего период собственных продольных колебаний 7*^ — 4 с на волне Л**30 м.
Решение (рис. 11.12). Находим точку Е пересечения горизонтали А.*=30 м с кривой т*“4с. Точка пересечения этой горизонтали с кривой т=»4 с в случае обгона судном волны лежит за пределами диаграммы, т. е. соответствует скорости, превышающей 24 уз. Через точку £ проводим вертикальную линию. Сочетания курсовых углов и скоростей, при которых конец вектора скорости попадет на эту вертикальную линию, точно соответствует резонансу килевой качки.
По верхней вспомогательной шкале находим значение т, отвечающее границам . резонансной зоны. При Тф«*4 с они приближенно равны 3,1 и 5,7 с. Находя на гори* зонтали А.=*30 м точки Е\ и £2, соответствующие этим значениям т, проводим через них вертикальные линии, ограничивающие резонансную зону.
В целях избежания усиленной килевой качки следует выбирать курс так, чтобы вектор скорости судна оканчивался вне указанной зоны. Однако учитывая, что в положении лагом или почти лагом к волне амплитуды килевой качки не могут достигать больших значений, такие сочетания курсов и скоростей, при которых вектор скорости оканчивается в секторе 78°<<7<102°, являются допустимыми в смысле килевой качки даже если они принадлежат резонансной зоне.
Следует отметить, что информацию о резонансной зоне, полученную с диаграммы, не всегда можно использовать с высокой степенью эффективности. Это объясняется тем, что ввиду относительно малого значения периода собственных продольных колебаний судна зоны килевой качки оказываются настолько широкими, что для выхода за их пределы иногда требуются чрезвычайно большие изменения курсовых углов и скоростей, вплоть до поворота на обратный курс. Кроме того, из-за большого демпфирования амплитуда килевой качки не имеет такого острого пика при резонансе, как амплитуда бортовой качки, поэтому небольшие изменения курса и скорости весьма эффективны для уменьшения бортовой качки, и не сильно сказываются на килевой.
Несмотря на это, знание неблагоприятных сочетаний курса и скорости, соответствующих резонансу килевой качки, дает судоводителю возможность принимать решения о выборе метода штормования. Если, например, известно, что резонанс наступает на встречном волнении, то это является основанием для того, чтобы предпочесть штор- мование на попутном волнении. Если известны резонансные сочетания курса и скорости, то становится ясным, в какую сторону изменять фактические курс и скорость, чтобы, если и не выйти за пределы резонансной зоны, то по крайней мере не ухудшить положения судна. Если, например, резонанс наступает при отсутствии хода (кривая г =Т+ пересекается с прямой, отвечающей данной длине волны, непосредственно на оси ординат), то уменьшение скорости судна\ зачастую предпринимаемое судоводителями в условиях тяжелого иггорма, поставит судно не в лучшие, а в худшие условия. Такого случая для морских транспортных судов следует ожидать, когда (8-г-10)ГСр при плавании в грузу и (11-7-13) ГСр при плавании в балласте.
Кроме того, при резонансе сдвиг фаз килевой качки по отношению к волце близок к 90°. Это означает, что в момент нахождения впадины или гребня волны у миделя судно имеет наибольший дифферент на нос или на корму. При таком угле сдвига фаз принципиально невозможно выбрать курсовые углы, которые одновременно соответствовали бы выгодным условиям в отношении перемещений носа и
кормы: при любой длине волны курсовые углы, наиболее благоприятные для носовой оконечности, оказываются самыми неблагоприятными для кормы, и наоборот.

 Максимальная потеря скорости судна на волнении также наблюдается при резонансе килевой качки. Эти обстоятельства лишний раз указывают на то, что штормование в резонансном режиме килевой качки ставит судно в очень тяжелые условия и поэтому должно быть исключено.
Максимальная потеря скорости судна на волнении также наблюдается при резонансе килевой качки. Эти обстоятельства лишний раз указывают на то, что штормование в резонансном режиме килевой качки ставит судно в очень тяжелые условия и поэтому должно быть исключено.
Можно отметить, что для любого морского транспортного судна с осадкой до 16—18 м резонанс килевой качки не наступает на волнах любой длины, если судно идет на чисто попутном волнении и при этом его скорость превышает 8—9 уз.
Пример 3. Определить положение первой и второй резонансных зон дли судна, имеющего период собственных
г».Л ,, ,0 „ колебаний Г о «16 с; при значительной
Рис. I!13. К определению резонансных кур- , 4 , ‘
Дата добавления: 2016-07-09; просмотров: 1040;
