Метод, основанный на использовании теории графов

Не составляя и не решая дифференциальных или ин­тегральных уравнений, можно получить количественные характеристики надежности восстанавливаемых резерви­рованных устройств.

Непосредственно по известному графу состояний за­писываются выражения для установившегося значения коэффициента готовности, а также выражения в преобра­зованиях Лапласа для вероятности безотказной работы и вероятности застать устройство в исправном состоянии в любой момент времени.

Рассмотрим эту методику на частном примере.

Пусть дано некоторое устройство (элемент, узел, блок, система и т. п.), для повышения надежности ко­торого применено общее постоянное резервирование.

Из­вестны:

- интенсивности перехода устройства из i-го состоя­ния в состояния i-1 и i+1;

- необходимое время работы устройства;

- кратность резервирования;

- число обслуживающих бригад.

Необходимо вычислить вероятность безотказной ра­боты Р(t) в течение времени t и вероятность 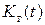того, что резервированное устройство будет исправно в любой момент времени

Решение. Сделаем следующие допущения:

- длительность безотказной работы и время восста­новления отдельных элементов подчиняются экспоненци­альному закону;

- при отказе одного из устройств оно сразу же от­правляется на восстановление и ожидает очереди на об­служивание, если все ремонтные бригады заняты, или немедленно начинается процесс восстановления, если очереди на обслуживание нет.

При указанных выше допущениях функционирование резервированного устройства можно представить уже известным графом, изображенным на рис.31.

В дальнейшем для конкретности предположим, что кратность резервирования m=2, все устройства равнонадежны, каждое из них имеет интенсивность отказов l, а при отказе любого из устройств надежность исправных не меняется. Предположим, что резервированная си­стема обслуживается одной бригадой, а интенсивность восстановления равна μ. Тогда граф рис. 31 преобра­зуется в граф, показанный на рис. 33.

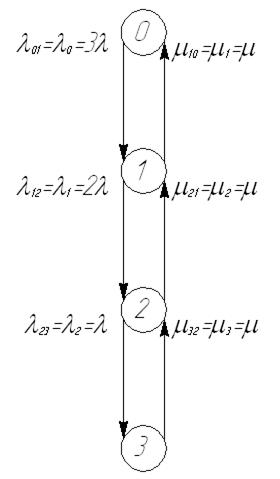
Рис.33. Граф переходов системы при двухкратном резервировании

Из нулевого состояния (все устройства исправны) возможен переход в состояние 1, когда одно устройство отказало и отправлено в ремонт, а два других исправны. Интенсивность перехода будет 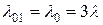. Из состояния 1 возможен переход либо в состояние 0 с интенсивностью восстановления 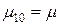, либо в состояние 2 с интенсив­ностью отказов 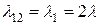. В состоянии 2 одно устройст­во исправно, одно ремонтируется и одно ожидает ре­монта.

Из состояния 2 вновь возможны два перехода: в со­стояние 1 с интенсивностью восстановления 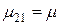(так имеется только одна ремонтная бригада) и в состояние 3 с интенсивностью перехода 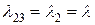. В состоянии 3 все устройства отказали, поэтому возможен переход только в состояние 2 с интенсивностью восстановления .

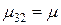Если имеется несколько бригад обслуживания, то вид графа не меняется, а изменяются лишь интенсивности пе­рехода 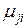. Так, например, если имеется две бригады об­служивания, то 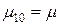, 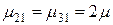. Если число бригад k=3, то 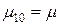, , 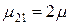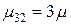. Вид графа также не из­меняется, если имеет место резервирование замещением. В этом случае 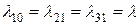(в предположении, что ин­тенсивности отказов резервных устройств до включения в работу равны нулю).

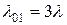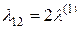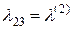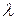Если отказ одного из устройств вызывает изменение интенсивности отказов устройств, оставшихся исправны­ми, то вид графа вновь не изменяется. В этом случае , , , где – интенсивность отказов любого из устройств, когда все они иcправны; 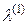– интенсив­ность отказов каждого из исправ­ных устройств при отказе любого одного; 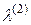–интенсивность от­казов исправного устройства при отказе двух любых устройств.

Рассмотрим, как деформиру­ется приведенный на рис. 33 граф в случае резервирования по схе­ме группирования (с дробной кратностью, когда m=1/2). Так как отказ наступает, когда отка­зывают любые два устройства, то при одной бригаде обслуживания , , , , .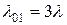

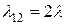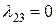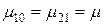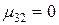Очевидно, что в этом случае граф будет иметь вид, показанный на рис.34.

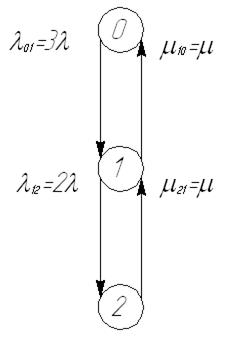
Рис.34. Граф переходов системы при общем резервировании с кратностью m=1/2

Не­зависимо от вида графа ясно, что для нахождения коли­чественных характеристик надежности перечисленных в нашем примере случаев достаточно было бы получить фор­мулы для вычисления вероятностей состояний устройства в зависимости от интенсивностей переходов 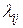и .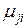

Получим расчетные формулы для коэффициента го­товности, вероятности застать систему в исправном со­стоянии в любой момент времени и вероятности безотказной работы системы.

Составим систему дифференциальных уравнений, опи­сывающих поведение такого устройства:

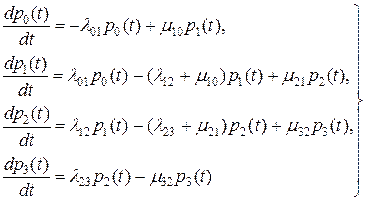(3.4.61)

Начальные условия: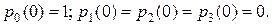

Решая эту систему уравнений с помощью преобразо­вания Лапласа, приходим к следующей системе линейных алгебраических уравнений:

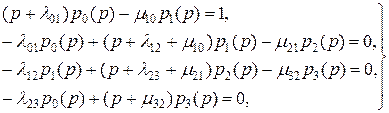(3.4.62)

где 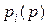– преобразования Лапласа вероятности .

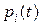Правило Крамера дает решение такой системы в виде

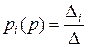(3.4.63)

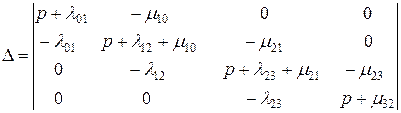(3.4.64)

где 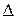– главный определитель системы; 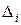– частный определитель, который находится из (3.4.64) заменой i-го столбца коэффициентами, стоящими в правых частях уравнений (3.4.62).

Раскрывая 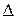по степеням p, получаем

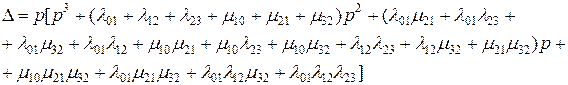(3.4.65)

Анализируя вид коэффициентов в определителе 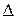, можно заметить, что они построены следующим образом. Свободный член равен 0. Это является необходимым условием существования стационарных решений для 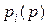так как

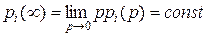
Коэффициент при 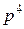равен 1. Коэффициент при 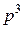пред­ставляет собой сумму всех интенсивностей переходов гра­фа рис.33. Коэффициент при 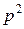есть сумма попарных произведений интенсивностей переходов, за исключением произведений вида 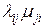и 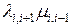. Наконец, коэффициент при 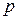есть сумма произведений интенсивностей пе­реходов, взятых по три, за исключением тех, в которых встречаются те же произведения 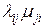и 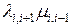, т. е., остаются только произведения интенсивностей переходов, из каждой крайней точки графа состояний в данную ( 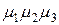– в точку 0, 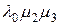– в точку 1, 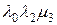– в точку 2, 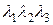– в точку 3).

В нашем случае имеется только одно отказовое со­стояние – состояние 3. Поэтому вероятность 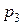есть ве­роятность простоя 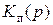, причем

,

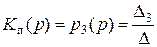где

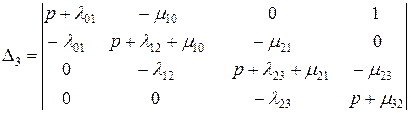(3.4.66)

Из выражения для 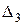видно, что этот определитель пред­ставляет собой произведение интенсивностей переходов из всех возможных исправных состояний в неисправное состояние 3.

Таким образом, для нашей задачи вероятность пре­бывания резервированной системы в состоянии 3 или ве­роятность простоя в преобразовании Лапласа будет иметь вид

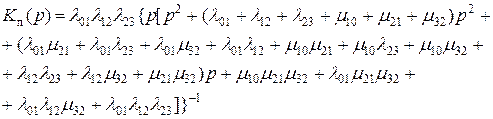(3.4.67)

Если известно 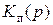, то вероятность застать систему в исправном состоянии находится из выражений

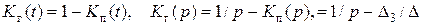(3.4.68)

Установленное нами правило для системы, граф со­стояний которой соответствует рис. 33, оказывается спра­ведливым для системы с произвольным числом состоя­ний, граф которой изображен на рис.31, т. е.

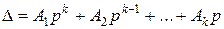, (3.4.69)

где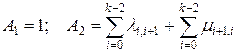

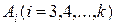– сумма произведений интенсивностей переходов, взятых по i-1, за исключением тех членов, в которых содержатся произведения вида 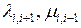(i=0,1,2,…,k-2).

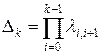
Граф состояний резервированной восстанавливаемой системы может иметь более сложный вид, чем показан­ный на рис.31. Сложные ветвящиеся графы получаются при раздельном резервировании, учете двух характеров отказов, отсутствии контроля моментов отказов отдель­ных устройств резервированной системы, резервировании неравнонадежных устройств и т. п.

В этих случаях может быть несколько отказовых со­стояний. Тогда вероятность того, что резервированная система будет неисправна в любой момент времени t, равна

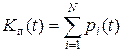(3.4.70)

где 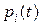– вероятность того, что система в момент вре­мени t находится в i-м отказовом состоянии; N — число отказовых состояний.

Очевидно, что преобразование Лапласа для 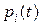на­ходится из выражения

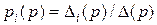
где 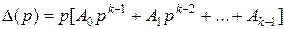– главный определитель системы; 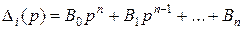– частный определитель; 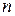– число, зависящее от уровня отказового состояния; 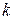– число состояний системы.

Нами установлено, что независимо от вида графа ре­зервированной восстанавливаемой системы коэффициен­ты 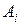определителя 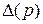находятся по указанному выше правилу.

Оказывается, что число n и коэффициенты частно­го определителя 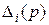легко находятся непосредственно из графа и выражений для коэффициентов A при соот­ветствующих степенях p определителя 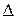. Степень поли­нома числителя определяется из выражения

,

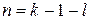где 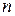– число состояний устройства, равное числу узлов графа; 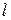– номер уровня i-го отказового состояния, чис­ленно равный количеству неисправных устройств резер­вированной системы, находящейся в отказовом состоя­нии i.

Коэффициент 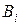определителя 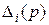находится непо­средственно из коэффициента 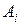при той же степени p определителя 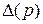. Оказывается, что 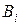содержит те члены коэффициента 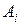, в которых имеются произведе­ния всех интенсивностей переходов из состояния 0(все элементы исправны) в отказовое состояние i по кратчай­шему пути, т. е. без восстановления.

Описанная методика позволяет особенно легко найти установившееся значение функции готовности – коэффи­циент готовности.

Так как

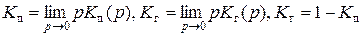(3.4.71)

то

,

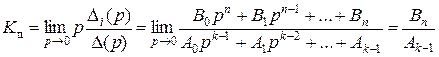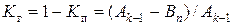
Для нашего примера

.

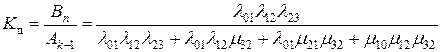По известной функции готовности легко также найти вероятность безотказной работы. Очевидно, что в графе состояний теперь будут отсутствовать переходы из отка­зовых состояний всего устройства в исправные. Тогда для отыскания преобразования Лапласа вероятности отказа достаточно в выражении для 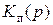вычеркнуть члены, которые содержат интенсивности переходов из отказо­вых состояний системы в исправные во всех коэффициентах 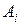и 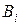. В нашем примере необходимо вычеркнуть члены, в которых содержится коэффициент . Тогда из выражения для 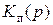получим

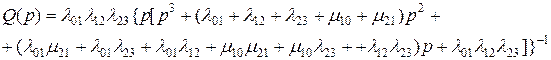
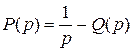
Зная 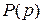, легко найти среднюю наработку до первого отказа.

Так как

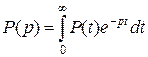, (3.4.72)

то

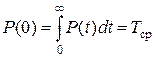(3.4.73)

т. е. для определения средней наработки до первого от­каза достаточно найти преобразование Лапласа 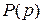и затем, подставляя в него p=0, записать выражение для средней наработки до первого отказа.

Для нашего примера из выражения для 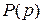имеем

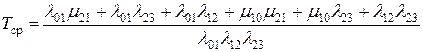
Описанный метод расчета надежности резервирован­ных восстанавливаемых устройств позволяет найти рас­четные соотношения непосредственно из графа состояний системы, не составляя и не решая уравнений массового обслуживания. Его недостаток в том, что для определе­ния 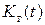и 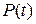необходимо находить обратные преоб­разования Лапласа от функци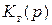й и 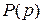представ­ляющих собой дробно-рациональные функции.