Закон Гесса и следствия из него. Применение закона Гесса для расчета изменения энтальпии химической реакции
а) В основе термохимических расчетов лежит закон, открытый русским ученым Г. И. Гессом в 1840 г. Закон гласит: тепловой эффект реакции зависит от вида и состояния исходных веществ и конечных продуктов, но не зависит от пути перехода (из начального состояния в конечное).
Или иначе: тепловое эффект реакции равен алгебраической сумме тепловых эффектов всех его промежуточных стадий:
ΔН = ΔН1 + ΔН2.
Следствия из закона Гесса:
1. Если в результате последовательных химических реакций система приходит в состояние, полностью совпадающее с исходным (круговой процесс), то сумма тепловых эффектов этих реакций будет равна нулю.
2. Тепловой эффект реакций (ΔНх.р.) равен сумме теплот образования (или ΔНобр.) конечных веществ (ΔНконеч. в-в) за вычетом суммы теплот образования исходных веществ (ΔНисх. в-в):
ΔНх.р. = Σ ΔНпрод. р-ции – Σ ΔНисх. в-в.
б) Наиболее важное для практики следствие закона Гесса: - энтальпия химической реакции равна разности между суммой энтальпий образования продуктов реакции минус и суммой энтальпийи образования исходных веществ (реагентов).  (2.6)
(2.6)
Например, значение энтальпии реакции между растворами сильной кислоты и сильного основания может быть получено по табличным данным энтальпий образования исходных веществ., если представить эту реакцию:, например HCl(р-р) + NaOH(р-р) = NaCl(р-р) + Н2Ож может быть получено по табулированным энтальпиям образования в виде реакций между ионами, поскольку эта реакция в действительности является реакцией между ионами H+ и OH–: H+(р-р) + OH–(р-р) = Н2Ож (2.7) Уравнение (2.7) - это уравнение реакции нейтрализации. Оно справедливо для всех реакций между сильной кислотой и сильным основанием, а следовательно и энтальпия этих реакцийодно и тоже для будет одна и та же.Табличные значения энтальпий образования ( 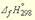 ) ионов Н+ и ОН– и молекулы Н2Ож известны и соответственно равны 0, –229,94 и –285,84 кДж/моль, соответственно. Тогда, по формуле (2.6) тепловой эффект реакции нейтрализации:
) ионов Н+ и ОН– и молекулы Н2Ож известны и соответственно равны 0, –229,94 и –285,84 кДж/моль, соответственно. Тогда, по формуле (2.6) тепловой эффект реакции нейтрализации:
 rHо =
rHо =  fH(H2Oж ) –
fH(H2Oж ) –  fH(H+р-р) –
fH(H+р-р) –  fH(OH–р-р ) =–285,84 – (–229,94) = –55,9 кДж/моль
fH(OH–р-р ) =–285,84 – (–229,94) = –55,9 кДж/моль
Стандартная энтропия веществ. Изменение энтропии при изменении агрегатного состояния вещества. Расчет изменения стандартной энтропии химической реакции. Влияние температуры на величину свободной энергии Гиббса и константу равновесия
а) Л. Больцман определил энтропию как термодинамическую вероятность состояния (беспорядок) системы W. Энтропия связана с термодинамической вероятностью соотношением:
|
Размерность энтропии 1 моля вещества совпадает с размерностью газовой постоянной R и равна Дж∙моль–1∙K–1. Изменение энтропии *) в необратимых и обратимых процессах передается соотношениями ΔS > Q / T и ΔS = Q / T. Например, изменение энтропии плавления равно теплоте (энтальпии) плавления ΔSпл = ΔHпл/Tпл. Для химической реакции изменение энтропии аналогично изменению энтальпии 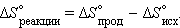
*) термин энтропия был введен Клаузиусом (1865 г.) через отношение Q / T (приведенное тепло).
Здесь ΔS° соответствует энтропии стандартного состояния. Стандартные энтропии простых веществ не равны нулю. В отличие от других термодинамических функций энтропия идеально кристаллического тела при абсолютном нуле равна нулю (постулат Планка), поскольку W = 1. Энтропия вещества или системы тел при определенной температуре является абсолютной величиной. В табл. 4.1 приведены стандартные энтропии S° некоторых веществ.
|
Из табл. следует, что энтропия зависит от:
· агрегатного состояния вещества. Энтропия увеличивается при переходе от твердого к жидкому и особенно к газообразному состоянию (вода, лед, пар).
· изотопного состава (H2O и D2O).
· молекулярной массы однотипных соединений (CH4, C2H6, н-C4H10).
· строения молекулы (н-C4H10, изо-C4H10).
· кристаллической структуры (аллотропии) – алмаз, графит.
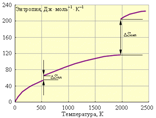
Наконец, рис. 4.3 иллюстрирует зависимость энтропии от температуры.
|
| Зависимость энтропии от температуры для свинца:ΔSпл = 8 Дж·моль–1·К–1; Tпл = 600,5 К;ΔSкип = 88 Дж·моль–1·К–1; Tкип = 2013 К |
Следовательно, стремление системы к беспорядку проявляется тем больше, чем выше температура. Произведение изменения энтропии системы на температуру T ΔSколичественно оценивает эту тендецию и называется энтропийным фактором.
б) Для реакции, протекающей в изобарно-изотермических условиях, в некотором неравновесном исходном состоянии энергии Гиббса или химические потенциалы реагирующих веществ и продуктов реакции в общем случае не одинаковы, их разность (ΔGT) может быть рассчитана по уравнению:

где  — отношение парциальных давлений участников реакции в исходном состоянии в степенях, равных их стехиометрическим коэффициентам; R —универсальная газовая постоянная.
— отношение парциальных давлений участников реакции в исходном состоянии в степенях, равных их стехиометрическим коэффициентам; R —универсальная газовая постоянная.
Это уравнение называют уравнением изотермы химической реакции. Оно позволяет рассчитать изменение энергии Гиббса при протекании процесса и определить направление протекания реакции:
при 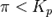
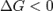 — реакция идёт в прямом направлении, слева направо;
— реакция идёт в прямом направлении, слева направо;
при 
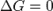 — реакция достигла равновесного состояния;
— реакция достигла равновесного состояния;
при 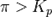
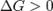 — реакция идёт в обратном направлении.
— реакция идёт в обратном направлении.
Стандартная константа равновесия связана со стандартной энергией Гиббса реакции соотношением:
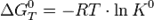
Стандартная энергия Гиббса реакции в газовой смеси — энергия Гиббса реакции при стандартных парциальных давлениях всех компонентов, равных 0,1013 МПа (1 атм).
Стандартная энергия Гиббса реакции в растворе — энергия Гиббса при стандартном состоянии раствора, за которое принимают гипотетический раствор со свойствами предельно разбавленного раствора, но с концентрацией всех реагентов, равной единице. Величина стандартной энергии Гиббса реакции может быть использована для приближенной оценки термодинамической возможности протекания реакции в данном направлении, если начальные условия не сильно отличаются от стандартных. Кроме того, сравнивая величины стандартной энергии Гиббса нескольких реакций, можно выбрать наиболее предпочтительные, для которых 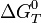 имеет наибольшую по модулю отрицательную величину.
имеет наибольшую по модулю отрицательную величину.
Дата добавления: 2016-07-09; просмотров: 9411;

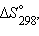 (Дж∙моль–1∙K–1)
(Дж∙моль–1∙K–1)