Модель оптимального размера заказа с количественными скидками.
Предположим, что:
1) темп спроса на товар известен и постоянен;
2) время выполнения заказа известно и постоянно.
Исходные данные: темп спроса, издержки заказа, издержки хранения, цена товара, количественные скидки в случае закупки крупных партий товара.
Результат: оптимальный размер заказа, время между заказами, точка восстановления запаса, количество заказов за фиксированный период времени, совокупные издержки.
Пусть Q — размер заказа;
T — продолжительность периода планирования;
D, d —величина спроса за период планирования и в единицу времени соответственно;
К — издержки одного заказа;
Н, h — удельные издержки хранения за период и в единицу времени соответственно.
Предположим, что известны числа сi, аi, i = 1, ..., п, где сi — цена продукта при размере заказа Q в интервале ai–1£ Q < аi. Будем считать, что a0 = 0 и an = +¥.
Тогда:

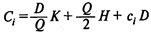
Оптимальный размер заказа определяется в результате решения п задач. Каждая из этих задач сводится к определению такого размера заказа Qi, i = 1,..., п, при котором функция совокупных (общих) издержек 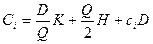 достигает минимума при ограничениях
достигает минимума при ограничениях 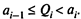
Решение исходной задачи определяется из условия
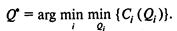
На рис. 6 изображены функции совокупных издержек для трех значений цен продукта. Значение цены c1 определено на интервале 0 £ Q < а1, цены с2 — на интервале a1 £ Q < а2, цены c3 — на интервале a2 £ Q < +¥.
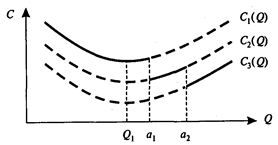
Рис. 6
Соответственно, функция общих издержек C1(Q) определена при значении цены с1 на интервале 0 £ Q < а1, функция C2(Q) — при значении цены с2 на интервале a1 £ Q < а2, функция C3(Q) — при значении цены c3 на интервале a2 £ Q < +¥.
Минимальное значение функции C1(Q) в области ее допустимых значений достигается в точке Q1, функции C2(Q) — в точке а1, функции C3(Q) — в точке а2.
Оптимальный размер заказа следует выбирать из величин Q1, a1 и a2 по формуле
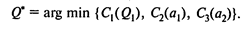
Дата добавления: 2016-07-09; просмотров: 1230;
