Необходимые и достаточные признаки устойчивости линейных стационарных САУ

Для определения устойчивости САУ необходимо решить характеристическое уравнение и определить корни. Рассмотрим, каким условиям должны удовлетворять корни характеристического уравнения, чтобы система была устойчивой. Будем называть корни с отрицательными вещественными частями левыми, так как они расположены на комплексной плоскости корней слева от мнимой оси, а корни с положительными вещественными частями – правыми корнями.

Для этого рассмотрим различные случаи.

Вещественным корням характеристического уравнения 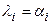соответствуют слагаемые, представляющие собой экспоненты .

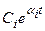Очевидно, отрицательным (левым) корням 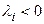соответствуют затухающие экспоненты (рис.8.2,а), положительным (правым) корням 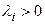– возрастающие экспоненты (рис.8.2,б) и при нулевых корнях слагаемые представляют собой прямые, параллельные оси времени (рис.8.2,в).

Комплексные корни характеристического уравнения всегда бывают попарно сопряженными 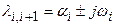. Слагаемые, определяемые этими корнями, представлены в виде

,

где 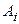и 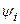– новые постоянные.

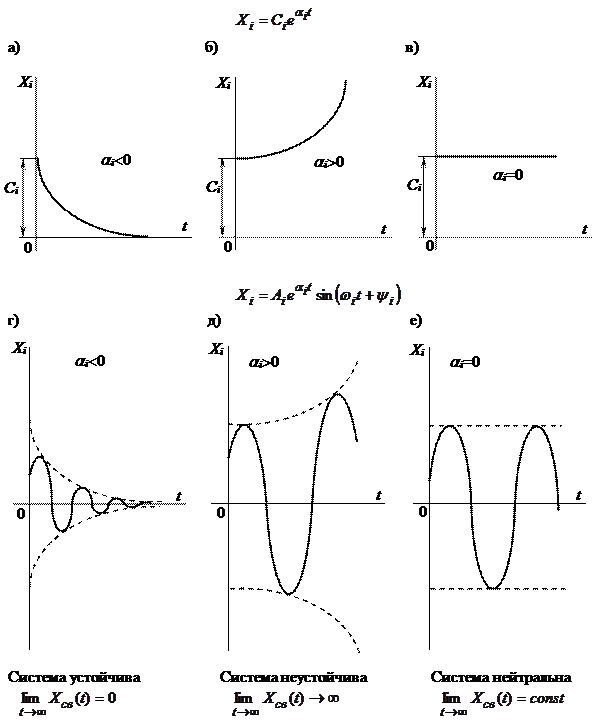Рис.8.2. Графики свободного движения САУ

В этом случае при получаются затухающие колебания (рис.8.2,г), при получаются расходящиеся колебания (рис.8.2,д) и при 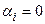– незатухающие колебания (рис.8.2,г).

Для устойчивости и в этом случае необходимо выполнение условия .

Таким образом, необходимое и достаточное условие устойчивости формулируется следующим образом: для того, чтобы линейная система была асимптотически устойчива, необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части, т.е. были левыми.

Вычисление корней весьма просто лишь для характеристического уравнения первой и второй степеней. Существуют общие выражения для определения корней уравнений третьей и четвертой степеней, но эти выражения громоздки и практически мало пригодны. Что же касается уравнений более высоких степеней, то для них практически невозможно написать общие выражения для вычисления корней через коэффициенты характеристического уравнения. Поэтому весьма важное значение приобретают правила, которые позволяют определить устойчивость системы без вычисления корней. Такие правила называют критериями устойчивости.

С помощью критериев устойчивости можно не только установить, устойчива система или нет, но и выяснить, как влияют на устойчивость те или иные параметры элементов и структурные изменения в системе.

Критерии устойчивости могут быть разделены на алгебраические и частотные.

Алгебраические критерии устойчивости определяют условия устойчивости в виде алгебраических неравенств, составленных из коэффициентов характеристического уравнения системы.

Частотные критерии устойчивости выражаются в виде условий, которым должны удовлетворять частотные характеристики системы для того, чтобы система была устойчива. Из частотных критериев устойчивости будем рассматривать критерий устойчивости Михайлова и критерий устойчивости Найквиста.

Однако все критерии устойчивости эквивалентны независимо от их природы, ибо определяют условия, при которых корни характеристического уравнения САУ имеют отрицательные вещественные части.