Понятие устойчивости процесса управления. Определение устойчивости по Ляпунову. Формулировка первой и второй теорем Ляпунова и их значение

На любую САУ всегда действуют различные возмущения, которые могут нарушить ее нормальную работу. Для того чтобы любая САУ была работоспособна, она прежде всего должна быть устойчивой. САУ устойчива, если она обладает способностью (свойством) возвращаться (с определенной точностью) в состояние равновесия после снятия внешних воздействий, которые вывели ее из этого состояния. Если система неустойчива, то она не возвращается в исходное состояние, из которого ее вывели, а либо удаляется от него, либо совершает вокруг него недопустимо большие колебания. Устойчивость является важной динамической характеристикой САУ.

В общем случае, рассматривая нелинейные системы, вводят понятия устойчивости “в малом”, ”в большом” и “в целом”. Система устойчива “в малом”, если констатируют лишь факт наличия области устойчивости, но не определяют ее границы. Система устойчива “в большом”, когда определены границы области устойчивости и реальные начальные отклонения не выводят ее из этой области. Систему называют устойчивой “в целом”, когда САУ возвращается в исходное состояние при любых начальных отклонениях.

В качестве простейшего примера можно рассматривать состояние шара, изображенного на рис. 8.1. Положение равновесия шара определяется точкой A₀. Случай, изображенный на рис. 8.1,а, соответствует устойчивости “в целом”, ибо при любом отклонении шара от положения равновесия он возвращается в конечную область, окружающую точку равновесия A₀, или в точку A₀ при отсутствии сил трения. Случай, изображенный на рис. 8.1,г, может соответствовать либо устойчивости ”в большом”, либо устойчивости ”в малом”. Если система линейная устойчива ”в целом”, то она устойчива ”в большом” и ”в малом”, а система, устойчивая ”в большом”, будет устойчива и ”в малом”. Случай, изображенный на рис. 8.1,б, соответствует неустойчивому положению равновесия, а на рис. 8.1,в – безразличному равновесию.

В рассмотренном примере с шаром вопрос об устойчивости решается довольно просто. Система будет устойчива, если из возмущающего состояния (для шара точка A₁ или A₂ на рис. 8.1,а) она перейдет в некоторую заданную область, окружающую невозмущенное состояние равновесия (точка A₀).

В общем случае далеко не всегда ясно, при каких условиях равновесное положение системы будет устойчивым.

Впервые математическое и в то же время удобное с инженерной точки зрения определение устойчивости было дано выдающимся русским математиком А.М.Ляпуновым в 1892 году в работе “Общая задача об устойчивости движения”. Определение устойчивости А.М.Ляпуновым оказалось настолько удачным и наилучшим образом, удовлетворяющим многим техническим задачам, что оно и в настоящее время принято как основное.

Рассмотрим для простоты САУ, имеющую один вход и один выход, дифференциальное уравнение которой имеет вид:

,

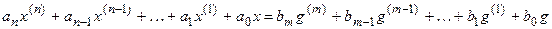где 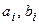– коэффициенты уравнения, определяемые параметрами системы;

x и g – выходная и входная переменные, причем .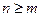

Рис. 8.1. Состояние равновесия шара:

а – устойчивое в целом; б – неустойчивое; в – безразличное;

г – устойчивое в большом; д – полуустойчивое.

Изменение регулируемой величины x(t) при произвольном внешнем воздействии g(t) представляет собой решение уравнения

.

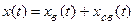Первое слагаемое 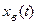– вынужденная составляющая, имеющая тот же характер, что и правая часть уравнения. Она определяется как частное решение неоднородного дифференциального уравнения, а второе слагаемое 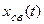– свободная (переходная) составляющая, которая определяется общим решением однородного дифференциального уравнения без правой части:

.

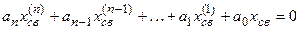Так как в ТАУ интересуются устойчивостью вынужденной составляющей 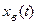переходного процесса, то за невозмущенное движение системы необходимо принять вынужденную составляющую переходного процесса 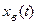. Тогда возмущенным движением будет любое положение, возможное в системе изменения регулируемой величины x(t), а отклонением или вариацией будет свободная составляющая

.

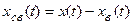В соответствии с определением устойчивости по А.М.Ляпунову система будет устойчивой, если с течением времени при 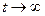свободная составляющая будет стремиться к нулю, т.е. 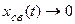. Чтобы найти эту составляющую, необходимо решить дифференциальное уравнение. Решение уравнения находят как

,

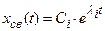где 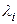– корни характеристического уравнения. Дифференцируя это выражение n раз и, подставляя в исходное уравнение, после сокращения на общий множитель 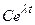получаем

.

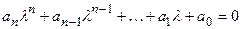Полученное алгебраическое уравнение является характеристическим уравнением, а его корни 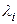определяют характер переходного процесса в системе.

Во многих случаях устойчивость движения исследуется по уравнениям первого приближения. Однако решения уравнений первого приближения могут дать иногда совершенно неверное заключение об устойчивости движения. Поэтому для исследования устойчивости систем по их линеаризованным уравнениям принципиально важны следующие теоремы А.М.Ляпунова, которые приведем без доказательств.

Теорема 1. Если вещественные части всех корней 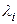характеристического уравнения первого приближения отрицательны, то возмущенное движение асимптотически устойчиво.

Теорема 2. Если среди корней 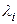характеристического уравнения первого приближения имеется хотя бы один корень с положительной вещественной частью, то невозмущенное движение неустойчиво.

Если среди корней характеристического уравнения имеется один или несколько нулевых корней, а вещественные части остальных корней отрицательны, то этот случай называют критическим. Как показал Ляпунов, в критическом случае устойчивость (неустойчивость) невозмущенного движения не может быть оценена по уравнениям первого приближения, и поэтому в данном случае требуется рассмотрение дифференциальных уравнений возмущенного движения в исходном виде.

Теоремы Ляпунова имеют весьма важное значение, так как они позволяют судить об устойчивости нелинейных систем по их линеаризованным уравнениям (уравнениям первого приближения).

Следовательно, для того, чтобы САУ выполняла свое назначение, необходимо, чтобы свободная (переходная) составляющая движения системы, возникающая в силу различных причин, с течением времени уменьшалась до нуля.

Линейная САУ называется устойчивой, если переходная составляющая движения (собственное движение) затухает, т.е.

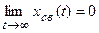. (8.1)

Если переходная составляющая движения расходится, т.е.

,

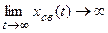то такая система называется неустойчивой системой.