электростатического поля

1. Энергия системы неподвижных точечных зарядов.Электростатические силы взаимо­действия консервативны. Следователь-но, система зарядов обладает потенци­альной энергией. Найдем потенциальную энергию системы двух неподвижных точеч­ных зарядов Q₁и Q₂,находящихся на расстоянии rдруг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией:

где j₁₂ и j₂₁ - соответственно потенциалы, создаваемые зарядом Q₂в точке нахожде­ния заряда Q₁и зарядом Q₁в точке нахождения заряда Q₂, причем

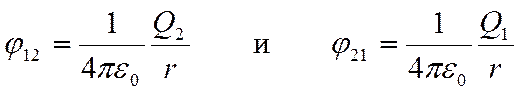
поэтому W₁ = W₂= W и

.

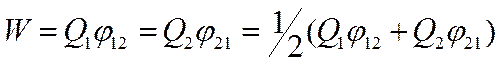Добавляя к системе из двух зарядов последовательно заряды Q₃, Q₄,…, можно убедиться в том, что в случае пнеподвижных зарядов энергия взаимодействия системы точечных зарядов равна

,

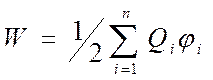где j_i - потенциал, создаваемый в той точке, где находится заряд Q_i всеми зарядами, кроме i-го.

2. Энергия заряженного уединенного проводника. Пусть имеется уединенный проводник, заряд, емкость и потенциал которого соответственно равны Q, С, j. Уве-личим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконеч­ности на уединенный проводник, затратив на это работу, равную

.

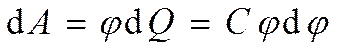Чтобы зарядить тело от нулевого потенциала до j,необходимо совершить работу

.

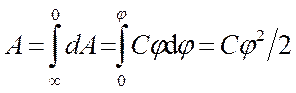Энергия заряженного проводника равна той работе, которую необходимо совер­шить, чтобы зарядить этот проводник:

.

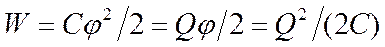3. Энергия заряженного конденсатора. Как всякий заряженный проводник, конден­сатор обладает энергией, которая в соответст-вии с предыдущей формулой равна

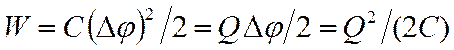
где Q — заряд конденсатора, С — его емкость, Dj — разность потенциалов между обкладками конденсатора.

Используя это выражение, можно найти механическую (пондеромоторную) силу, с которой пластины конденсаторапритягивают друг друга. Для этого предположим, что расстояние х между пластинами меняется, например, на величину dх. Тогда действующая сила совершает работу dA=Fdx вследствие уменьшения потенциальной энергии системы Fdx=-dW, откуда

.

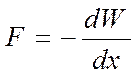Подставив в выражение для энергии заряженного конденсатора ( 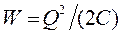) выражение для емкости плоского конденсатора ( 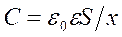), получим

.

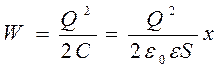Производя дифференцирование при кон-кретном значении энергии, найдем искомую пондеромоторную силу:

,

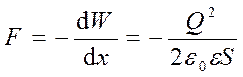где знак минус указывает, что сила F является силой притяжения.

4. Энергия электростатического поля. Преобразуем формулу 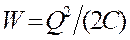, выражаю-щую энергию плоского конденсатора посредс-твом зарядов и потенциалов, воспользовав­шись выражением для емкости плоского конденсатора ( 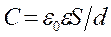)и разности потенци­а-лов между его обкладками (Dj=Ed).Тогда

,

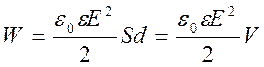где V=Sd - объем конденсатора. Эта формула показывает, что энергия конден­сатора выра-жается через величину, характеризующую электростатическое поле, - на­пряженность Е.

Объемная плотность энергии электро-статического поля (энергия единицы объема)

.

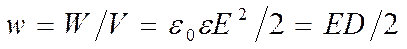Это выражение справедливо только для изотропного диэлектрика, для которого выполняется соотношение P=æE.

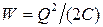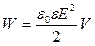Формулы и соответственносвязывают энергию конденсатора с зарядом на его обкладках и с напряженностью поля. Возникает, естественно, вопрос о локализа­ции электростатической энергии и что является ее носителем — заряды или поле? Ответ на этот вопрос может дать только опыт. Электростатика изучает постоянные во времени поля неподвижных зарядов, т.е. в ней поля и обусловившие их заряды неотделимы друг от друга. Поэтому электростатика ответить на поставленные воп­росы не может. Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать обособленно, незави­симо от возбудивших их зарядов, и распространяются в пространстве в виде электро­магнитных волн, способных переносить энергию. Это убедительно подтверждает основ­ное положение теории близкодействия о том, что энергия локализована в поле и что носителем энергии является поле.