Теорема Гаусса для электростатического
Поля в вакууме
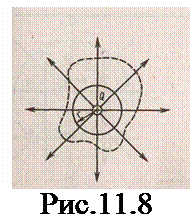 В соответствии с формулой (11.5) поток вектора напряженности сквозь сферическую поверхность радиуса r, охва-тывающую точечный заряд Q, находящийся в ее центре (рис.11.8), равен
В соответствии с формулой (11.5) поток вектора напряженности сквозь сферическую поверхность радиуса r, охва-тывающую точечный заряд Q, находящийся в ее центре (рис.11.8), равен
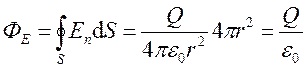 .
.
Этот результат справедлив для замкнутой поверхности любой формы.
Обобщая это выражение на систему точечных зарядов Q1, Q2, … , Qn с учетом суперпозиции полей получим:
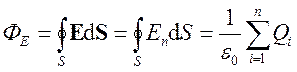 . (11.11)
. (11.11)
Формула (11.11) выражает теорему Гаусса для электростатического поля в вакууме.
Теорема гласит:поток вектора напряженно-сти электростатического поля в вакууме скво-зь произвольную замкнутую поверхность ра-вен алгебраической сумме заключенных внут-ри этой поверхности зарядов, деленной на e0.
Эта теорема выведена математически для векторного поля любой природы русским математиком М. В. Остроградским (1801—1862), а затем независимо от него применительно к электростатическому полю немецким ученым К. Гауссом (1777—1855).
В общем случае электрические заряды могут быть «размазаны» с некоторой объёмной плотностью 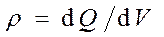 , различной в разных местах пространства. Тогда суммарный заряд, заключенный внутри замкнутой поверхности S , охватывающей некоторый объём V ,
, различной в разных местах пространства. Тогда суммарный заряд, заключенный внутри замкнутой поверхности S , охватывающей некоторый объём V ,
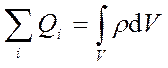 .
.
 Далее воспользовавшись теоремой Гаусса (11.11) можно записать
Далее воспользовавшись теоремой Гаусса (11.11) можно записать
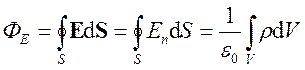 .
.
Дата добавления: 2016-06-24; просмотров: 544;
