Потенциал электростатического
Поля
Тело, находящееся в потенциальном поле сил (электростатическое поле является потен-циальным), обладает потенциальной энергией, за счет которой силами поля совершается работа. Работа консервативных сил совер-шается за счет убыли потенциальной энергии. Поэтому работу сил электростатического поля можно представить как разность потенциаль-ных энергий, которыми обладает точечный заряд Q0в начальной и конечной точках поля заряда Q:
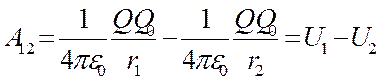 , (11.12)
, (11.12)
откуда следует, что потенциальная энергия заряда Q0в поле заряда Q равна
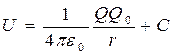 .
.
Она определяется неоднозначно, а с точнос-тью до произвольной постоянной С. Если считать, что при удалении заряда в бесконеч-ность (r®¥)потенциальная энергия обра-щается в нуль (U=0), то С=0 и потенциальная энергия заряда Q0находящегося в поле заряда Q на расстоянии r от него, равна
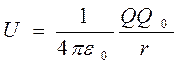 . (11.13)
. (11.13)
Для одноименных зарядов Q0Q>0и потенциальная энергия их взаимодействия (отталкивания) положительна, для разноимен-ных зарядов Q0Q<0и потенциальная энергия их взаимодействия (притяжения) отрицательна.
Если поле создается системой п точечных зарядов Q1, Q2, ..., Qnто работа электро-статических сил, совершаемая над зарядом Q0 равна алгебраической сумме работ сил, обус-ловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия U заряда Q0,находящегося в этом поле, равна сумме потен-циальных энергий Ui каждого из зарядов:
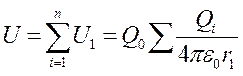 . (11.14)
. (11.14)
Из формул (11.13) и (11.14) вытекает, что отношение U/Q0не зависит от Q0 и является поэтому энергетической характеристикой электростатического поля, называемой потенциалом:
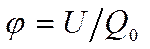 . (11.15)
. (11.15)
Потенциал j в какой-либо точке электро-статического поля есть физическая величина, определяемая потенциальной энергией еди-ничного положительного заряда, помещенного в эту точку.
Из формул (11.15) и (11.13) следует, что потенциал поля, создаваемого точечным зарядом Q, равен
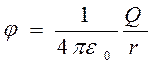 . (11.16)
. (11.16)
Работа, совершаемая силами электростати-ческого поля при перемещении заряда Q0 из точки 1 в точку 2, может быть представлена как
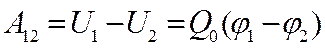 , (11.17)
, (11.17)
т.е. равна произведению перемещаемого заря-да на разность потенциалов в начальной и конечной точках.
Разность потенциаловдвух точек 1 и 2 в электростатическом поле определяется рабо-той, совершаемой силами поля, при переме-щении единичного положительного заряда из точки 1 в точку 2.
Работа сил поля при перемещении заряда Q0 из точки 1 в точку 2 может быть записана также в виде
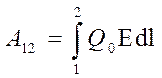 . (11.18)
. (11.18)
Приравняв (11.17) и (11.18), придем к выражению для разности потенциалов:
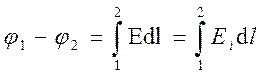 , (11.19)
, (11.19)
где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения.
Если перемещать заряд Q0из произволь-ной точки за пределы поля, т.е. в бесконечность, где, по условию, потенциал равен нулю, то работа сил электростатического поля, согласно (11.17), A¥=Q0j,откуда
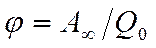 . (11.20)
. (11.20)
Таким образом, потенциал — физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки поля в бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.
Из выражения 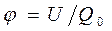 (11.15) следует, что единица потенциала — вольт (В): 1 В есть потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В = 1 Дж/Кл). Учитывая размерность вольта, можно показать, что единица напряженности электростатического поля действительно равна 1 В/м:
(11.15) следует, что единица потенциала — вольт (В): 1 В есть потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В = 1 Дж/Кл). Учитывая размерность вольта, можно показать, что единица напряженности электростатического поля действительно равна 1 В/м:
1 Н/Кл=1 Н∙м/(Кл∙м)=1 Дж/(Кл∙м)=1 В/м.
 Из формул (11.14) и (11.15) вытекает, что если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:
Из формул (11.14) и (11.15) вытекает, что если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:
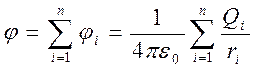 .
.
Дата добавления: 2016-06-24; просмотров: 536;
