Параллельное соединение конденсаторов

Электрическая емкость уединенного

Проводника

Рассмотрим уединенный проводник, т.е. проводник, который удален от других провод­ников, тел и зарядов. Его потенциал, согласно

прямо пропорционален заряду проводника. Из опыта следует, что разные проводники, буду-чи одинаково заряжен­ными, имеют различные потенциалы. Поэтому для уединенного проводника можно, записать

Величину

называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника определяется заря-дом, сообщение которого проводнику изме­няет его потенциал на единицу.

Емкость проводника зависит от его разме-ров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциала.

Единица электроемкости - фарад(Ф): 1 Ф - емкость такого уединенного провод­ника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл.

Потенциал уединенного шара радиуса R, находящегося в однород­ной среде с диэлект-рической проницаемостью e, равен

.

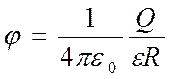Отсюда следует, что емкость шара

.

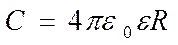Следовательно емкостью 1 Ф обладал бы уединенный шар, находящийся в ваку­уме и имеющий радиус R=С/(4pe₀) » 9∙10⁶ км. Это примерно в 1400 раз больше радиуса Земли (электроемкость Земли С » 0,7 мФ). Таким образом, фарад -очень большая величина, поэтому на практике используются дольные единицы — миллифа­рад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ). Из последнего выражения также вытекает, что единица электрической постоянной e₀ - фарад на метр (Ф/м)

Конденсаторы

Для того чтобы проводник обладал боль-шой емкостью, он должен иметь очень большие размеры. На практике, необходимы устройства, об­ладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, т.е. обладать большой емкостью. Эти устройства получили название конденсаторов.

Конденсатор состоит из двух проводников (обкладок), разделенных диэлектриком. На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому провод-никам придают такую форму, чтобы поле, создаваемое накапливаемыми заря­дами, было сосредоточено в узком зазоре между обклад-ками конденсатора. Этому условию удовлет-воряют: 1) две плоские пластины; 2) два коак-сиальных цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические.

Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (j₁-j₂)между его обкладками:

.

Рассчитаем емкость плоского конденса-тора, состоящего из двух параллельных метал-лических пластин площадью S каждая, распо-ложенных на расстоянии d друг от друга и имеющих заряды +Q и -Q. Если расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффек-тами можно пренебречь и поле между обкладками считать однородным. При наличии диэлектрика между обкладками разность потен­циалов между ними, согласно

,

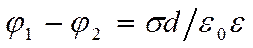где e — диэлектрическая проницаемость. Тогда, заменяя Q=sS в выражение для емкос-ти и подставляя туда же выражение для разности потенциалов,получим выражение для емкости плоского конденсатора:

.

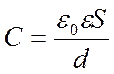Рассуждая аналогично можно получить выражения для емкости цилиндрического и сферического конденсаторов:

,

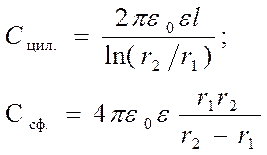где в первом случае r₁ и r₂ (r₂>r₁) – радиусы двух полых коаксиальных цилиндров, выполняющих роль обкладок конденсатора, а l их длина; во вторам случае r₁ и r₂ (r₂>r₁) – радиусы двух концентрических сферических обкладок; e - диэлектрическая проницаемость диэлектрика между обкладками конденсатора.

Для увеличения емкости и варьирования её возможных значений конденсаторы соеди-няют в батареи, при этом используется их па-раллельное и последовательное соединения.

Параллельное соединение конденсаторов

Параллельное соединение конденсаторов представлено на рис.13.4.

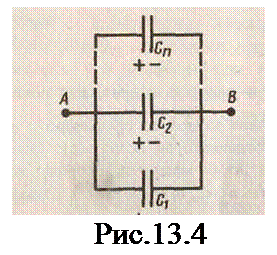У параллельно соединен-ных конденсаторов раз-ность потенциалов на обкладках конденсато-ров одинакова и равна j_А‑j_В. Если емкости отдельных конденсато-ров С₁, С₂, ..., С_n то их заряды равны

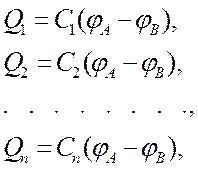
а заряд батареи конденсаторов

.

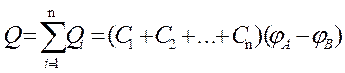Полная емкость батареи

.

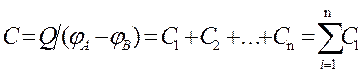т.е. при параллельном соединении конденса-торов она равна сумме емкостей отдель­ных конденсаторов.