Передаточные функции АСР
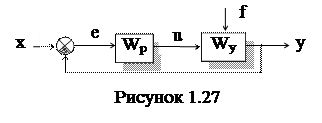 Для исследования и расчета структурную схему АСР путем эквивалентных преобразований приводят к простейшему стандартному виду «объект - регулятор» (см. рисунок 1.27). Практически все инженерные методы расчета и определения параметров настройки регуляторов применены для такой стандартной структуры.
Для исследования и расчета структурную схему АСР путем эквивалентных преобразований приводят к простейшему стандартному виду «объект - регулятор» (см. рисунок 1.27). Практически все инженерные методы расчета и определения параметров настройки регуляторов применены для такой стандартной структуры.
В общем случае любая одномерная АСР с главной обратной связью путем постепенного укрупнения звеньев может быть приведена к такому виду.
Если выход системы у не подавать на ее вход, то получается разомкнутая система регулирования, передаточная функция которой определяется как произведение:
W¥ = Wp.Wy
(Wp - ПФ регулятора, Wy - ПФ объекта управления).


|
|




|
Фз(s) = 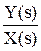 =
= 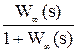 .
.
(далее будем рассматривать только системы с обратной отрицательной связью, поскольку они используются в подавляющем большинстве АСР).
Данная передаточная функция Фз(s) определяет зависимость у от х и называется передаточной функцией замкнутой системы по каналу задающего воздействия (по заданию).
Для АСР существуют также передаточные функции по другим каналам:
Фe(s) = 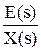 =
= 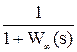 - по ошибке,
- по ошибке,
Фв(s) = 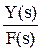 =
= 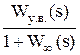 - по возмущению,
- по возмущению,
где Wу.в.(s) – передаточная функция объекта управления по каналу передачи возмущающего воздействия.
В отношении учета возмущения возможны два варианта:
- возмущение оказывает аддитивное влияние на управляющее воздействие (см. рисунок 1.29,а);
- возмущение влияет на измерения регулируемого параметра (см. рисунок 1.29,б).
Примером первого варианта может быть влияние колебаний напряжения в сети на напряжение, подаваемое регулятором на нагревательный элемент объекта. Пример второго варианта: погрешности при измерениях регулируемого параметра вследствие изменения температуры окружающей среды. Wу.в. – модель влияния окружающей среды на измерения.
 | |||
 |
а) б)
Рисунок 1.29
Для первого варианта передаточная функция Wу.в. принимается равной Wу, для второго – как правило, на схеме она выделена в отдельное звено.
Поскольку передаточная функция разомкнутой системы является в общем случае дробно-рациональной функцией вида W¥ = 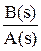 , то передаточные функции замкнутой системы могут быть преобразованы:
, то передаточные функции замкнутой системы могут быть преобразованы:
Фз(s) = 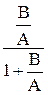 =
= 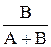 =
= 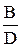 , Фe(s) =
, Фe(s) = 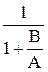 =
= 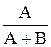 =
= 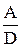 ,
,
где D = A + B.
Как видно, эти передаточные функции отличаются только выражениями числителей. Выражение знаменателя называется характеристическим выражением замкнутой системы и обозначается как Dз(s) = A(s) + B(s), в то время как выражение, находящееся в знаменателе передаточной функции разомкнутой системы W¥, называется характеристическим выражением разомкнутой системы А(s).
Пример. Определение передаточных функций АСР.
Структура АСР представлена на рисунке 1.30. Требуется определить передаточные функции регулятора, объекта, разомкнутой системы, замкнутой системы и характеристические выражения.
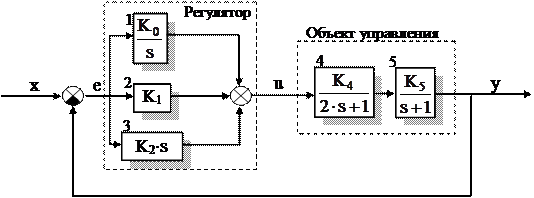 |
Рисунок 1.30
Параметры K0 = 1, K1 = 3, K2 = 1,5, K4 = 2, K5 = 0,5.
В структурной схеме АСР звенья, соответствующие регулирующему устройству, стоят перед звеньями объекта управления и генерируют управляющее воздействие на объект u. По схеме видно, что к схеме регулятора относятся звенья 1, 2 и 3, а к схеме объекта – звенья 4 и 5.
Учитывая, что звенья 1, 2 и 3 соединены параллельно, получаем передаточную функцию регулятора как сумму передаточных функций звеньев:
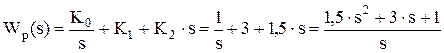 .
.
Звенья 4 и 5 соединены последовательно, поэтому передаточная функция объекта управления определяется как произведение передаточных функций звеньев:
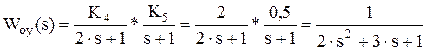 .
.
Передаточная функция разомкнутой системы:
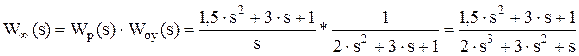 ,
,
откуда видно, что числитель В(s) = 1,5.s2 + 3.s + 1, знаменатель (он же характеристический полином разомкнутой системы) А(s) = 2.s3 + 3.s2 + s. Тогда характеристический полином замкнутой системы равен:
D(s) = A(s) + B(s) = 2.s3 + 3.s2 + s + 1,5.s2 + 3.s + 1 = 2.s3 + 4,5.s2 + 4.s + 1.
Передаточные функции замкнутой системы:
по заданию 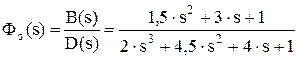 ,
,
по ошибке 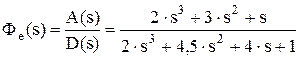 .
.
При определении передаточной функции по возмущению принимается Wу.в. = Wоу. Тогда
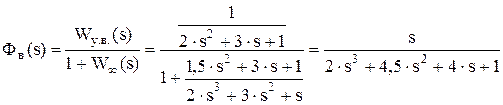 . ¨
. ¨
Дата добавления: 2016-06-24; просмотров: 860;
