Пример θ – соединение.
Рассмотрим следующий запрос. Пусть отношение R15 содержит перечень деталей с указанием материалов, из которых эти детали изготавливаются, и оно имеет вид:
| R15 | |||
| Шифр детали | Название детали | Материал | |
| Гайка M1 | сталь-ст1 | ||
| Гайка М2 | сталь-ст2 | ||
| Гайка М3 | сталь-ст1 | ||
| Болт М1 | сталь-ст3 | ||
| Болт М3 | сталь-ст3 | ||
| Шайба М1 | сталь-ст1 | ||
| Шайба М3 | сталь-ст1 | ||
| Гайка М4 | сталь-ст2 | ||
| Болт М2 | сталь-ст3 | ||
| Болт М5 | сталь-ст3 | ||
| Шайба М2 | сталь-ст1 | ||
| R17 | |||
| Название детали | |||
| Гайка M1 | |||
А отношение R16 содержит перечень цехов и шифров изготавливаемых в них деталей.
| R16 Шифр детали | Цех |
| Цех 1 | |
| Цех 3 Цех 1 |
Получим перечень деталей, которые изготавливаются в цеху 1 из материала "сталь-ст1".
R17= 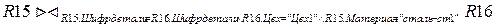 R18=
R18= 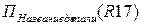
Естественным соединением 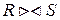 называется соединение по эквивалентности двух отношений R и S, выполненное по всем общим атрибутам X, из результатов которого исключается по одному экземпляру каждого общего атрибута.
называется соединение по эквивалентности двух отношений R и S, выполненное по всем общим атрибутам X, из результатов которого исключается по одному экземпляру каждого общего атрибута.
Естественное соединение – проекция выборки из декартова произведения.
Пример: 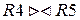
| R4 | |
| Шифр детали | Название детали |
| Гайка M1 | |
| Гайка М3 | |
| Болт М3 |
| R5 Шифр детали | Цех |
| Цех 1 | |
| Цех 3 Цех 1 |
R4  R5 R5
| ||
| Шифр детали | Название детали | Цех |
| Гайка M1 | Цех 1 | |
| Гайка М3 | Цех 3 |
Внешнее соединение
При соединении двух отношений может потребоваться, чтобы строка из одного отношения была представлена в результате соединения, даже если в другом отношении не совпадающего значения. Это достигается с помощью внешнего соединения.
Левым внешним соединением 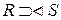 называется соединение, при котором кортежи отношения R, не имеющие совпадающих значений в общих атрибутах отношения S, также включаются в результирующее отношение.
называется соединение, при котором кортежи отношения R, не имеющие совпадающих значений в общих атрибутах отношения S, также включаются в результирующее отношение.
Для обозначения отсутствующих значений во втором отношении используется определитель Null.
Существует также правое внешнее соединение 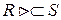 , когда в результирующем отношении содержатся все кортежи правого отношения.
, когда в результирующем отношении содержатся все кортежи правого отношения.
Полусоединение 
Операция полусоединения определяет отношение, которое содержит те кортежи отношения R, которые входят в соединение отношений R и S.
Операцию полусоединения можно сформулировать с помощью операторов проекции и соединения:
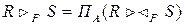
Здесь А – набор всех атрибутов в отношении R. Это полутета-соединение. Существуют полусоединения по эквивалентности и естественное полусоединение.
Последней операцией, включаемой в набор операций реляционной алгебры, является операция деления.
Пусть отношение R определено на множестве атрибутов A, а отношение S – на множестве атрибутов В, причем В 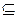 А. Пусть С=А – В, т.е. С является множеством атрибутов отношения R, которые не являются атрибутами отношения S. Тогда результатом деления R ÷ S является набор кортежей отношения R, определенных на множестве атрибутов C, которые соответствуют комбинации всех кортежей отношения S.
А. Пусть С=А – В, т.е. С является множеством атрибутов отношения R, которые не являются атрибутами отношения S. Тогда результатом деления R ÷ S является набор кортежей отношения R, определенных на множестве атрибутов C, которые соответствуют комбинации всех кортежей отношения S.
Операция деления может быть заменена последовательностью других операций:
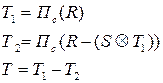
Пример.
Пусть делимое – отношение D1, содержащее номера поставщиков (SN) и номера поставляемых ими деталей (PN). Делители – отношения DOR, представленные ниже:
| SN | PN |
| S1 | P1 |
| S1 | P2 |
| S1 | P3 |
| S1 | P4 |
| S1 | P5 |
| S1 | P6 |
| S2 | P1 |
| S2 | P2 |
| S3 | P2 |
| S4 | P2 |
| S4 | P4 |
| S4 | P5 |
D1
DOR DOR DOR
| PN |
| P1 |
| P4 |
| PN |
| P1 |
| PN |
| P1 |
| P2 |
| P3 |
| P4 |
| P5 |
| P6 |
Результат деления D1 ÷ DOR:
| SN |
| S1 |
| S4 |
| SN |
| S1 |
| SN |
| S1 |
| S2 |
В последнем случае делителем является отношение, содержащее номера поставщиков, поставляющих все детали. Операция деления полезна именно для запросов такого рода. Если запрос на обычном языке включает слово «все» или «каждый» («получить поставщиков, поставляющих все детали»), то нужна операция деления.
Дата добавления: 2016-06-24; просмотров: 920;
