В первом примере , и мы убедились при анализе этой игры, что наилучшие стратегии игроков будут смешанные стратегии.

Во втором примере . Анализ игры показал, что наилучшими стратегиями будут чистые стратегии.

Если платёжная матрица игры обладает свойством , то такая игра называется с седловой точкой. На платёжной матрице такой игры существует элемент

.

Этот элемент называется седловой точкой, для которой справедливо неравенство

.

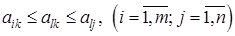Величина 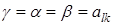называется чистой ценой игры. Пара стратегий 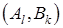является оптимальной парой, то есть образует решение игры 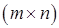среди чистых стратегий.

Теорема. Любая конечная парная игра с нулевой суммой и с полной информацией является игрой с седловой точкой.

Например, игры в шашки, шахматы являются конечными, парными играми с нулевой суммой и с полной информацией, поэтому они относятся к играм с седловой точкой.

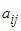
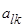
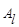
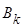
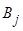
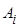
Графическая интерпретация игры с седловой точкой представлена на рисунке. Если игрок 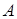допускает отклонение от своей оптимальной стратегии 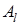, то он ухудшает свое положение, скатываясь по разрезу седла. Аналогично для игрока 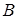, он будет увеличивать выигрыш игрока 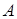, поднимаясь по профилю седла.

В теории игр доказывается, что каждая игра с полной информацией имеет седловую точку и следовательно, решение в чистых стратегиях. Другими словами, в каждой игре с полной информацией существует пара оптимальных стратегий той и другой стороны, дающая устойчивый выигрыш, равный чистой цене игры. Если игра с полной информацией состоит только из личных ходов, то при применении каждой стороной своей оптимальной стратегии игра должна кончаться всегда вполне определенным исходом, равным цене игры.

В качестве примера приведем следующую игру с полной информацией. Два игрока поочередно кладут одинаковые монеты на круглый стол, выбирая произвольно положение монеты (взаимное перекрытие монет не допускается). Выигрывает тот, кто положит последнюю монету (когда места для других уже не останется). Нетрудно убедиться, что исход этой игры предрешен, и существует определенная стратегия, обеспечивающая достоверный выигрыш тому из игроков, кто кладет монету первым. А именно, он должен первый раз положить монету в центр стола, а далее на каждый ход противника отвечать симметричным ходом. Очевидно, как бы ни вел себя противник, ему не избежать проигрыша. Поэтому игра имеет смысл только для лиц, не знающих ее решения. Точно так же дело обстоит с шахматами и другими играми с полной информацией; любая из этих игр обладает седловой точкой и, значит, решением, указывающим каждому игроку его оптимальную стратегию, так что игра имеет смысл только до тех пор, пока неизвестно решение. Решение шахматной игры не найдено (и в обозримом будущем вряд ли будет найдено) только потому, что число стратегий (комбинаций ходов) в шахматах слишком велико, чтобы можно было построить платежную матрицу и найти в ней седловую точку.