Решение игры среди чистых стратегий.
Рассмотрим игру 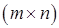 с платёжной матрицей:
с платёжной матрицей:
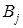
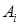
| 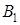
| ... | 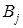
| ... | 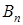
| ||
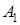
| 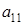
| ... | 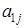
| ... | 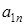
| 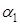
| |
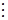
| 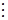
| ||||||
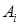
| 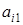
| ... | 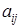
| ... | 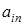
| 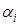
| 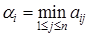
|
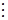
| 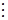
| ||||||
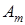
| 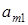
| ... | 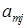
| ... | 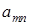
| 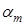
| |

| ... | 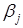
| ... | 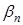
| 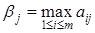
|
Если каждый из игроков выбирает одну из своих стратегий и в дальнейшем в процессе игры не может её менять, то говорят, что игрок применяет чистую стратегию. Необходимо определить наилучшие чистые стратегии игроков 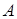 и
и 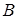 , которые в дальнейшем будут применяться постоянно. Под наилучшей чистой стратегией понимается стратегия, которая приносит игроку
, которые в дальнейшем будут применяться постоянно. Под наилучшей чистой стратегией понимается стратегия, которая приносит игроку 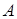 максимально возможный выигрыш (игроку
максимально возможный выигрыш (игроку 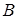 минимально возможный проигрыш).
минимально возможный проигрыш).
Вначале найдём наилучшую чистую стратегию игрока 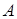 . Пусть он использует чистую стратегию
. Пусть он использует чистую стратегию 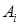 . Какой при этом у него будет гарантированный выигрыш? Очевидно, это будет зависеть от того, какую стратегию использует игрок
. Какой при этом у него будет гарантированный выигрыш? Очевидно, это будет зависеть от того, какую стратегию использует игрок 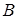 . Он может применять самую невыгодную для игрока
. Он может применять самую невыгодную для игрока 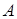 стратегию. Следовательно, гарантированный выигрыш игрока
стратегию. Следовательно, гарантированный выигрыш игрока 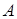 будет равен
будет равен
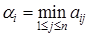 .
.
Но, так как он сам выбирает какую чистую стратегию использовать, то он будет применять ту чистую стратегию, которая даёт ему наибольший гарантированный выигрыш. Для этого ему нужно среди значений 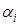
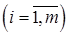 найти наибольший выигрыш
найти наибольший выигрыш 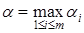 . Таким образом, гарантированный выигрыш игрока
. Таким образом, гарантированный выигрыш игрока 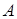 вычисляется как максимин на платёжной матрице:
вычисляется как максимин на платёжной матрице:
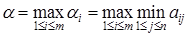 (1)
(1)
Пусть максимум по  в выражении (1) достигается при
в выражении (1) достигается при 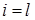 , то есть
, то есть 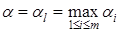 .
.
Тогда стратегия 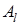 является наилучшей чистой стратегией игрока
является наилучшей чистой стратегией игрока 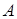 , и она называется максимальной стратегией, которая даёт игроку
, и она называется максимальной стратегией, которая даёт игроку 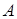 наибольший гарантированный выигрыш.
наибольший гарантированный выигрыш.
Величина  называется нижней ценой игры. При максиминной стратегии
называется нижней ценой игры. При максиминной стратегии 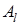 игрок
игрок 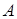 гарантирует себе выигрыш не меньший
гарантирует себе выигрыш не меньший  при любом поведении противника, поэтому величина
при любом поведении противника, поэтому величина  и называется «нижней ценой игры».
и называется «нижней ценой игры».
Теперь найдём наилучшую чистую стратегию игрока 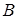 . Допустим он использует свою стратегию
. Допустим он использует свою стратегию 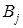 . Его проигрыш будет зависеть от действий игрока
. Его проигрыш будет зависеть от действий игрока 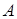 , который может применить стратегию, дающую ему наибольший выигрыш. Поэтому гарантированный проигрыш игрока
, который может применить стратегию, дающую ему наибольший выигрыш. Поэтому гарантированный проигрыш игрока 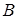 будет равен
будет равен
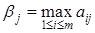
Естественно игрок 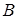 будет выбирать ту стратегию, которая обеспечит ему минимальный проигрыш. Величина гарантированного минимального проигрыша определяется как
будет выбирать ту стратегию, которая обеспечит ему минимальный проигрыш. Величина гарантированного минимального проигрыша определяется как
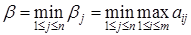 (2)
(2)
Пусть минимум по 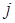 в выражении (2) достигается при
в выражении (2) достигается при 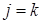 . Тогда стратегия
. Тогда стратегия 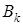 является наилучшей чистой стратегией игрока
является наилучшей чистой стратегией игрока 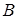 . Она называется минимальной стратегией, а величина игрока
. Она называется минимальной стратегией, а величина игрока 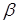 – верхней ценой игры.
– верхней ценой игры.
Можно показать, что для любой платёжной матрицы 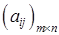 справедливо
справедливо  .
.
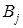
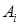
| 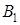
| ... | 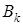
| ... | 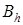
| ... | 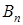
|
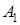
| |||||||
| |||||||
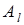
| 
| ... | 
| ||||
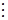
| 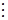
| ||||||
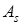
| 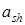
| ||||||
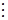
| |||||||
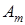
|
Действительно, пусть имеется матрица 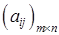 , для которой вычислены
, для которой вычислены

Элемент  является минимальным элементом строки
является минимальным элементом строки 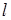 , поэтому имеет место неравенство
, поэтому имеет место неравенство 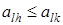 .
.
С другой стороны элемент 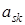 является максимальным элементом столбца
является максимальным элементом столбца 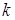 , поэтому имеет место неравенство
, поэтому имеет место неравенство 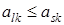 . Объединяя эти неравенства, получим неравенство вида
. Объединяя эти неравенства, получим неравенство вида
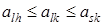 или
или  .
.
 Последнее неравенство означает, что
Последнее неравенство означает, что

Вычислим нижнюю и верхнюю цены игры для рассмотренных ранее примеров.
1. Игра в прятки. Нижняя цена игры
| 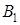
| 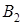
| |
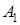
| -1 | 
| |

| -1 | 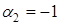
|

 .
.
Верхняя цена игры
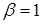 .
.
Следовательно 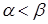 .
.
2. Игра «вооружение и самолёты».
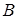
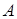
| 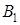
| 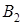
| 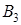
| 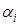
|
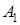
| 0,5 | 0,6 | 0,8 | 0,5 |

| 0,9 | 0,7 | 0,8 | 0,7 |
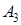
| 0,7 | 0,5 | 0,6 | 0,5 |
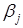
| 0,9 | 0,7 | 0,8 |
Нижняя цена игры
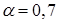 .
.
Верхняя цена игры
 .
.
Следовательно, справедливо равенство
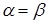 .
.
Дата добавления: 2016-05-16; просмотров: 722;
