Сила и установка распорных колец

Расчет плоских днищ основан на положениях классического курса «Сопротивление материалов», где выводятся формулы для определения напряжения в крупных пластинах, нагруженных равномерно распределенной нагрузкой. При этом рассматриваются следующие виды крепления пластин.

1. Пластина жестко закреплена по контуру:

s_max = 1,24 · Р · (R/h)². (5.1)

2. Шарнирная опора по контуру:

s_max = 0,75 · Р · (R/h)², (5.2)

где s_max – максимальные тангенциальные напряжения в пластине;

P – расчетное давление, МПа;

R– определяющий, геометрический размер пластины (радиус), м;

h – толщина пластины, м.

Вместо численного значения коэффициента, учитывающего способ закрепления пластины, введем коэффициент (К), а вместо радиуса (R) = D/2.

Тогда уравнения прочности пластин (5.1) и (5.2) можно представить в обобщенном виде:

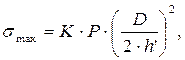(5.3)

где P – расчетное давление, МПа;

R– определяющий, геометрический размер оболочки (радиус), м;

h^/ – расчетная толщина пластины, равная h^/ = h – C;

С – конструктивная прибавка на коррозию принимаемая в зависимости от температурных условий работы конструкции в пределах 0,001 ÷ 0,004 м.

Для вывода уравнения прочности инженерного вида в выражении (5.3) максимальные тангенциальные напряжения (s_max)заменяем допускаемыми, которые в свою очередь снижаются в результате ослабления сварным швом:

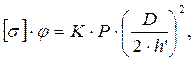(5.4)

[σ] – допускаемые напряжения, принимаемые по сортаменту стали;

j – коэффициент, учитывающий ослабление конструкции сварным швом, и принимающий в зависимости от вида шва следующие значения:

– стыковой двухсторонний шов автоматической сваркой, j = 1;

– стыковой односторонний шов автоматической сваркой, j = 0,9;

– стыковой ручной швов с двухсторонним проваром, j = 0,8.

– стыковой ручной шов с односторонним проваром, j = 0,7.

Подставляя в уравнение (5.4) значение h^/ = h – C и решая его относительно (h), будем иметь:

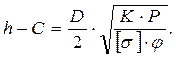(5.5)

С учетом коррозии получим:

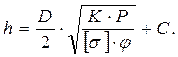(5.6)

Реальные конструкции днищ (болтовое крепление с прокладкой) трудно отнести к какому-либо варианту крепления. Поэтому на практике пользуются значением коэффициента (К), полученным по результатам экспериментальных испытаний. Можно выделить пять основных вариантов крепления фланца, которые представлены на рисунках 5.1 ÷ 5.5.

1. Плоский фланец и плоская крышка: Dрасч = DБ; K = 0,40.

Рисунок 5.1 – Схема крепления плоской крышки на плоском фланце

2. Плоский диск, зажатый между двумя фланцами: Dрасч = DС.П; К = 0,45.

Рисунок 5.2 – Схема нагружения диска, зажатого между двумя

фланцами

DВ

3. Плоская крышка крепится на болтах, а затяжка болтов вызывает изгиб фланца: D_расч = D_С.П.;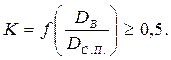

4. Днище, вваренное в корпус в «тавр»: Dрасч = DС.П; K = 0,6.

Рисунок 5.3 – Схема нагружения фланца, вызывающая его изгиб

Рисунок 5.4 – Схема нагружения днища, вваренного в корпус в «тавр»

5. Днище с отбортовкой и приваренное в «стык»: Dрасч = DВ – r; K = 0,45.

Рисунок 5.5 – Схема нагружения днища с отбортовкой, приваренного

в «стык»

Если в днище имеется неукрепленное отверстие, то толщина днища (h_o) увеличивается и определяется по формуле:

h_o = h/K_o, (5.7)

где К_о – коэффициент ослабления днища, зависящий от соотношения диаметров отверстия и днища (d/D):

К_о = 1 – 0,43 · (d/D), если d/D < 0,35; (5.8)

К_о = 0,85, если d/D > = 0,35,

где d – диаметр отверстия;

D – диаметр днища.

Конические днища применяются в цилиндрических вертикальных аппаратах для обеспечения выгрузки продукта. Для различных видов продуктов условия выгрузки регламентируются углом конусности днища (α):

– для липких и вязких продуктов 2 ∙ α = 60⁰;

– для хорошо сыпучих 2 ∙ α = 90⁰.

Расчет основан на мембранной теории оболочек. Уравнения мембраной теории приводятся к инженерному виду.

Рассмотрим цилиндрический аппарат с коническим днищем, нагруженным внутренним давлением.

Для тонкостенной оболочки произвольной формы (мембраны) тангенциальные (s_t), меридиональные (s_m), и радиальные (s_R) напряжения будут соответственно равны:

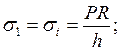
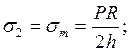
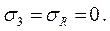
где P – расчетное давление, МПа;

R– определяющий, геометрический размер оболочки (радиус), м;

h – толщина оболочки, м;

Расчетная схема конического днища представлена на рисунке 5.6.

Рисунок 5.6 – Расчетная схема конического днища

Для рассматриваемой схемы нагружения оболочки геометрический радиус конуса равен:

R_к = ρ_t,(5.9)

где ρ_t – гангенциальный радиус конической оболочки.

Текущее значение радиуса оболочки (R_i) может быть определено из выражения:

R_i = y ∙ tg α, (5.10)

где y – текущее значение высоты конической оболочки.

Тангенциальный радиус конической оболочки из геометрии прямоугольного треугольника будет равен:

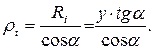
(5.11)

Тогда тангенциальные и меридиональные напряжения будут соответственно равны:

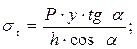
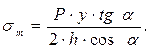(5.12)

Как следует из полученных формул, наиболее опасными, то есть максимальные по своей величине, являются тангенциальные напряжения (s_t), которые и принимаются в качестве расчетных для дальнейших преобразований.

В зависимости от расположения опор формулы для расчёта толщины стенки будут иметь различный вид.

1. Опоры расположены значительно выше конической части днища аппарата, нагруженного внутренним давлением. В этом случае текущая высота конической оболочки будет равняться своей максимальной величине, то есть:

у = H₂ – полная высота конического днища.

Тогда: 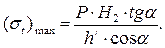(5.13)

По теории наибольших касательных напряжений ответственность за разрушение несут эквивалентные напряжения, которые определяют по формуле:

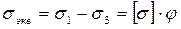. (5.14)

Подставляя значение допускаемых напряжений из формулы (5.14) в уравнение (5.13), получим:

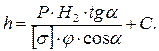(5.15)

2. Оболочка нагружена только гидростатическим давлением столба жидкости, которое определяется формулой вида Р = 10·ρ_ж·Н. В этом случае давление на вертикальную стенку на различных уровнях определяется по формуле:

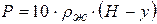. (5.16)

Определим текущее значение высоты (y), на которой напряжения достигают своего опасного максимума (σ_t = max). Подставляя значение гидростатического давления в формулу тангенциальных напряжений (5.12) будем иметь:

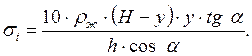(5.17)

С целью определения максимума полученной функции продифференцируем уравнение (5.17) по (dy) и приравняем результат к нулю.

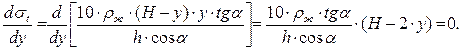(5.18)

Анализ полученного выражения показывает, что оно равняется нулю при y = H/2. Подставляя это соотношение и значение допускаемых напряжений ([σ]∙j) в уравнение (5.17), получаем выражение вида:

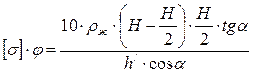. (5.19)

Решая уравнение (5.19) относительно (h^/) и учитывая надбавку на коррозию, получим:

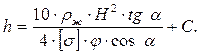(5.20)

3. Если цилиндрическая часть оболочки невелика, то есть Н/2 < Н₂, то максимальное напряжение будет наблюдаться в точке сопряжения конуса с цилиндром и составит:

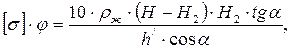(5.21)

Откуда: 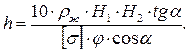(5.22)

4. Опоры конструкции установлены выше сопряжения конуса с цилиндром и над слоем жидкости действует избыточное давление Р₀. В этом случае вместо Н₁ в расчетное уравнение надо подставить приведенную высоту:

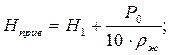(5.23)

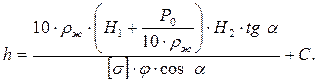(5.24)

5. В случае расположения опор ниже линии сопряжения стенки днища будут испытывать сжатие. Расчетная схема нагружения рассматриваемого варианта представлена на рисунке 5.7.

Рисунок 5.7 – Расчетная схема нагружения конического днища

на низких опорах

Для рассматриваемой схемы нагружения толщина стенки оболочки определяется по формуле:

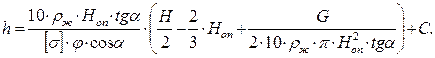(5.25)

При наличии на поверхности жидкости газового давления (Р_о) в расчётную формулу (5.25) подставляется вместо проектной высоты (Н) приведённая высота:

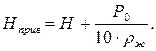(5.26)

Традиционной схемой установки опор является их крепление на цилиндрической части аппарата, то есть выше сопряжения. В том случае в коническом днище будут действовать растягивающие меридиональные напряжения. Расчетная схема нагружения оболочки на высоких опорах показана на рисунке 5.8.

Рисунок 5.8 – Расчетная схема оболочки на высоких опорах

Распределённая растягивающая сила (S₀) будет равна:

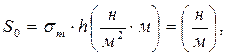(5.27)

где h – расчётная толщина оболочки.

Распорная распределённая сила, которая действует в горизонтальной плоскости, определяется из треугольника сил:

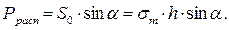(5.28)

Распределённая растягивающая сила (S₀) может быть определена из условия равновесия сил при мысленно отсечённой конической части:

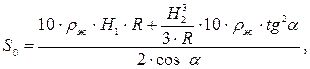(5.29)

где Н₁ – высота цилиндрической части;

Н₂ – высота конической части.

В случае если распорная сила достигает величины, которая превышает расчетное значение, устанавливается распорное кольцо. Схемы установки распорных колец показаны на рисунке 5.9.

Рисунок 5.9 – Схемы установки распорных колец

Сечение распорного кольца определяют на основании следующих допущений. Считается, что на кольцо действует равномерно распределённая нагрузка, отнесённая к единице длины.

Распорное давление на единицу площади кольца по контуру оболочки будет составлять:

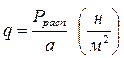. (5.30)

Возникающие от распорного давления тангенциальные напряжения будут равны:

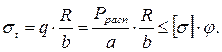(5.31)

Откуда площадь сечения кольца будет составлять:

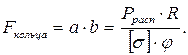(5.32)

Для того чтобы уменьшить распределённую распорную силу и устранить краевой эффект, рекомендуется применять днища с отбортовкой и плавным переходом к цилиндрической части. Схема днища с отбортовкой показана на рисунке 5.10.

Рисунок 5.10 – Схема днища с отбортовкой

Толщина стенок конической и цилиндрической частей днища с отбортовкой определяется на основании основного уравнения прочности из формулы:

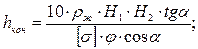(5.33)

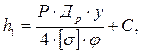(5.34)

где 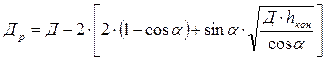; (5.35)

y – коэффициент формы днища, определяемый по графику.

Согласно норм Госгорэнергонадзора, сварные контуры оболочки должны располагаться на расстоянии не менее 50 мм от дуги в обе стороны. На расстояниях √Д·h₁ и √Д·h₁/cos α от дуги не должно быть вырезов и местных швов.

В этой зоне нельзя располагать опорные устройства.

Выпуклые днища требуют более высокого уровня технологии при их

производстве (литье, штамповка), однако в результате особенностей геометрических форм они не создают источников концентрации напряжений и поэтому способны выдерживать более высокие удельные нагрузки.

Существуют следующие виды конструкций выпуклых днищ: полушаровые, коробовые и эллиптические.

Полушаровое днище представляет собой полусферу, для которой тангенциальные напряжения равны меридиональным и составляют:

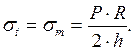(5.36)

Выполняя подстановки и преобразования аналогичные решениям, рассмотренным выше, получим рабочую формулу толщины оболочки:

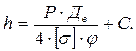(5.37)

В случае, если давление создано жидкостью, обладающей плотностью (ρ_ж), уравнение (5.37) принимает вид:

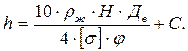(5.38)

При наличии газового давления над слоем жидкости получаем уравнение вида:

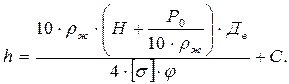(5.39)

Полушаровые днища применяются в технологических аппаратах с диаметром корпуса более 2,5 м.

Коробовые днища, представляющие собой сегментный срез от сферы,

применяют в отдельных случаях для снижения весогабаритных характеристик установки. Схема коробового днища показана на рисунке 5.11.

Рисунок 5.11 – Схема коробового днища

Толщину стенки коробового днища определяют по формуле:

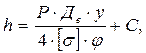(5.40)

где y – коэффициент формы днища, принимаемый по графику.

Для стандартных днищ принято соотношение Н/Д = 0,25.

Недостатком коробового днища является то обстоятельство, что в зоне сопряжения оболочек может возникать краевой эффект концентрации напряжений.

Эллиптические днища являются наиболее часто встречающимся вариантом выпуклых днищ. Профиль такого днища имеет геометрию полу-эллипса. Для эллиптических днищ также принято соотношение Н/Д = 0,25.

Схема эллиптического днища показана на рисунке 5.12.

Рисунок 5.12 – Схема эллиптического днища

Толщину стенки эллиптического днища определяют по формуле:

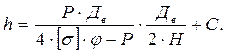(5.41)

Если в днище имеются отверстия, то в расчетную формулу вводится коэффициент ослабления днища отверстиями (z):

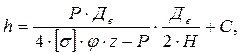(5.42)

где z = 1 – d / Д_в;

d – диаметр или сумма диаметров отверстий.

Нормативные требования к выпуклым днищам состоят в следующем:

1. ;

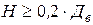2. Минимально допустимые расстояния от границы сверления до края оболочки (Δ₁) и между соседними сверлениями (Δ₂) определяются соотношениями, представленными на рисунке 5.13.

.

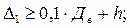
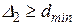Рисунок 5.13 – Координатная схема отверстий выпуклого днища

3. Длина отбортованной части конического днища принимается в зависимости от толщины стенки оболочки:

а) h ≤ 10 мм; L ≥ 25;

б) h = 10 ÷ 20 мм; L ≥ 40 мм;

в) h > 20 мм; L > 50 мм.

В отдельных случаях, в целях упрощения технологии изготовления, применяются сферические неотбортованные днища. Толщина стенки неотбортованного днища рассчитывается по формуле:

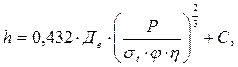(5.43)

где φ – коэффициент ослабления конструкции сварным швом;

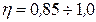– коэффициент, определяющий условия работы аппарата.