И предельно допустимой скорости вращения
Условия прочности быстровращающихся деталейзаключаются в обеспечении неразрушения конструкции при максимальной рабочей скорости ее вращения.
Расчет этих узлов (например, дисков центробежных распылительных мазутных форсунок) является очень ответственным видом расчета. Последнее связано с тем, что аварии такого оборудования могут иметь тяжелые последствия: повреждение экранных поверхностей топки котла и выход котла из строя; опасность для обслуживающего персонала. Расчетная схема быстровращающегося диска представлена на рисунке 7.1.

Рисунок 7.1 – Расчетная схема быстровращающегося диска
Рассмотрим диск толщиной (в), вращающийся с постоянной скоростью (w = const). Выделим на нем бесконечно малый элемент на радиусе r.
Пусть требуется определить напряжения (радиальные и тангенциальные) и обеспечить условие механической прочности диска.
Имеем дело с двухосным напряженным состоянием и к нему применим закон Гука. То есть относительные удлинения по расчетным осям будут определяться по формулам:

Из уравнения (7.1)радиальные напряжения определяют по формуле:
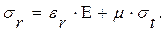 (7.3)
(7.3)
Подставляя полученное значение (σr) в уравнение (7.2), получим:
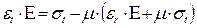 или
или 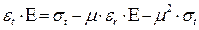 (7.4)
(7.4)
Решая уравнения (7.4) относительно (σt)и (σr)будем соответственно иметь:
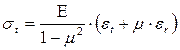 и аналогично
и аналогично 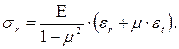 (7.5)
(7.5)
То есть для определения радиальных и тангенциальных напряжений необходимо знать соответствующие относительные деформации  и
и  . Для определения относительных деформаций составляем расчетную схему, которая представлена на рисунке 7.2.
. Для определения относительных деформаций составляем расчетную схему, которая представлена на рисунке 7.2.
В соответствии с принятой схемой относительные радиальные деформации будут равны:
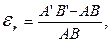 (7.6)
(7.6)
где А'В' = u+ du– (u– dr);
u – величина перемещения.

Рисунок 7.2 – Расчетная схема для определения радиальных
и тангенциальных относительных деформаций
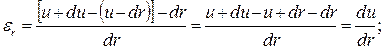 (7.7)
(7.7)
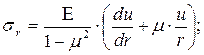 (7.8)
(7.8)
 (7.9)
(7.9)
 (7.10)
(7.10)
Определяем значения относительных деформаций для перемещения (u).
С этой целью воспользуемся принципом Д' Аламбера, в соответствие с которым рассмотрим равновесие элементарного объема, приложив к нему в качестве внешней силы соответствующую инерционную нагрузку. Тогда:
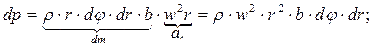 (7.11)
(7.11)
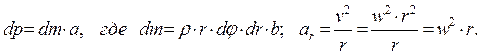 (7.12)
(7.12)
Для того чтобы рассмотреть уравнение равновесия спроецируем все силы на биссектрису угла dj. Расчетная схема уравнения равновесия представлена на рисунке 7.3.
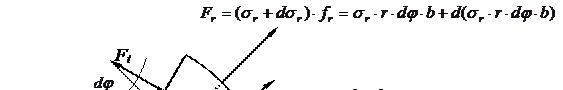
Рисунок 7.3 – Расчетная схема уравнения равновесия сил
на биссектрису угла dj
Результирующая сила от дифференциала радиальных напряжений в соответствии с расчетной схемой будет равна:
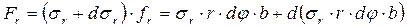 . (7.13)
. (7.13)
Запишем уравнение равновесия сил:
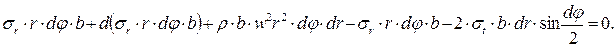
(7.14)
Для малых углов можно принять, что 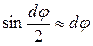 .
.
Тогда, сокращая уравнение (7.14) на 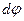 и b, получим:
и b, получим:
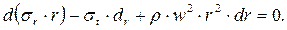 (7.15)
(7.15)
Разделим уравнение (7.15) на (dr) и поменяем знаки:
 (7.16)
(7.16)
Подставляя в полученное уравнение выражения (st) и (sr), получим:
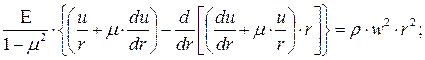 (7.17)
(7.17)
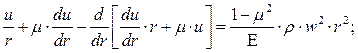 (7.18)
(7.18)
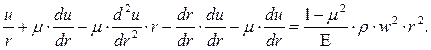 (7.19)
(7.19)
Меняя знаки в уравнении (7.19) и выполняя деление на (r), будем иметь:
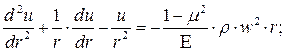 (7.20)
(7.20)
Левая часть уравнения (7.20) является результатом дифференцирования выражения вида:
 (7.21)
(7.21)
Выражение в квадратных скобках в левой части уравнения (7.21), в свою очередь, является результатом дифференцирования произведения вида:
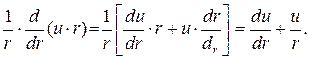 (7.22)
(7.22)
Производя последовательные подстановки левых частей уравнений (7.22) в (7.21), а затем в (7.21) в (7.20), получаем результирующее дифференциальное уравнение быстровращающегося диска вида:
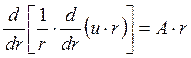 , (7.23)
, (7.23)
где  (7.24)
(7.24)
Допускаемые напряжения, толщина диска, его наружный диаметр и предельно допустимая скорость вращения определяются на основании результатов общего решения дифференциального уравнения быстровращающегося диска (7.23).
Задачу решаем двукратным интегрированием:
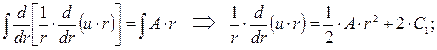 (7.25)
(7.25)
 (7.26)
(7.26)
Откуда 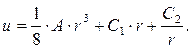 (7.27)
(7.27)
Относительные радиальные и тангенциальные деформации будут соответственно равны:
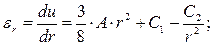 (7.28)
(7.28)
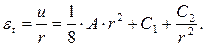 (7.29)
(7.29)
Радиальные и тангенциальные напряжения определяем по формулам:
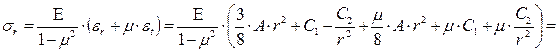

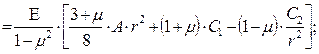 (7.30)
(7.30)

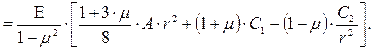 (7.31)
(7.31)
Постоянные интегрирования (С1) и (С2) определяют из граничных условий.
Рассмотрим эти частные решения дифференциального уравнения вращающегося диска. Эпюры радиальных и тангенциальных напряжений диска показаны на рисунке 7.4.

Рисунок 7.4 – Эпюры радиальных и тангенциальных напряжений диска
1. Константа интегрирования (С2) принимается равной нулю, исходя из физических представлений и математического анализа уравнения перемещений (7.27). Из этого уравнения следует, что если допустить С2 ¹0, то тогда деформации в центре диска должны достигнуть бесконечности, что по физическим представлениям невозможно. То есть, если r= 0, то 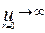 .
.
2. На наружной поверхности диска отсутствуют воздействия от соседних слоев в радиальном направлении, поэтому для них  .
.
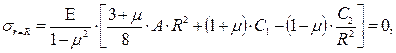 (7.32)
(7.32)
где С2 = 0 и тогда уравнение (7.32) принимает вид:
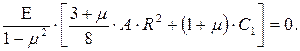 (7.33)
(7.33)
Сокращая уравнение (7.33) на первый сомножитель и решая его относительно (С1), получим:
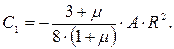 (7.34)
(7.34)
Подставляя полученное значение константы (С1) в уравнения для расчета радиальных (7.30) и тангенциальных (7.31) напряжений, будем иметь:
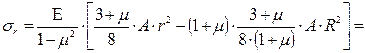
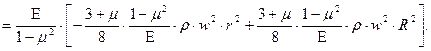 (7.35)
(7.35)
После сокращений и алгебраических преобразований уравнение (7.35) принимает вид:
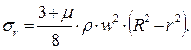 (7.36)
(7.36)
Принимая для стального диска (m= 0,3), получим расчетное уравнение инженерного вида:
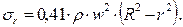 (7.36)
(7.36)
Анализ полученной формулы показывает, что на наружной поверхности (r = R) напряжения равны 0, а в центре диска, где r = 0, они достигают максимального значения.
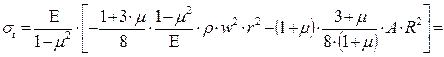
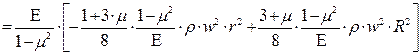 . (7.37)
. (7.37)
После сокращений и алгебраических преобразований уравнение (7.37) принимает вид:
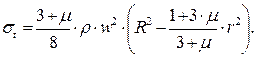 (7.38)
(7.38)
Анализ полученной формулы показывает, что в центре диска тангенциальные напряжения достигают своего максимума и определяются по формуле:
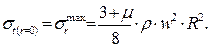 (7.39)
(7.39)
Принимая для сталей коэффициент Пуассона m = 0,3, получим расчетное уравнение инженерного вида:
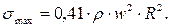 (7.40)
(7.40)
3. Величина перемещений определяется из анализа формулы (7.27), в соответствии с которой:
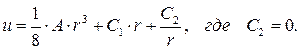
Подставляя в формулу (7.27) значения комплекса (А) (формула 7.24) и константу интегрирования (С1) (формула 7.34), получим:
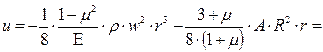
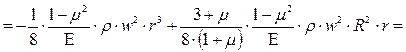
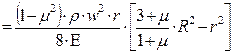 . (7.41)
. (7.41)
После сокращений и алгебраических преобразований получим выражение, имеющее вид:
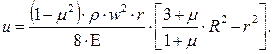 (7.42)
(7.42)
Анализ полученной формулы показывает, что в центре диска (r = 0) перемещения равны нулю (u = 0).
При R = r, будем иметь максимум перемещений:
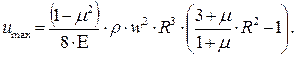 (7.43)
(7.43)
Принимая для сталей коэффициент Пуассона m = 0,3, получим окончательное выражение инженерного вида:
 (7.44)
(7.44)
Дата добавления: 2016-06-13; просмотров: 929;
