Двухволновом смятии
Если давление (Р) постепенно увеличивать, то при некотором критическом давлении (РКр) кольцо может сплющиться. Принимая в качестве расчетной схему нагруженного бруса, такое критическое давление определяем по формуле:
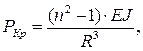 (6.3)
(6.3)
где ЕJ – жесткость бруса.
Подставляя в формулу (6.3) значение (n = 2), получим:
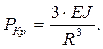 (6.4)
(6.4)
Полученная формула применима для цилиндрических оболочек, нагруженных наружным критическим давлением (РКр).
Подставляя в формулу (6.4) вместо жесткости бруса (EJ) цилиндрическую жесткость 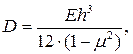 будем иметь:
будем иметь:
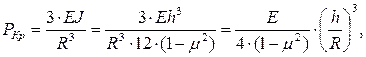 (6.5)
(6.5)
где μ – коэффициент Пуассона (коэффициент поперечной деформации или модуль упругости второго рода).
Производя в последнем выражении замену (R = D/2), после сокращений получим формулу Бресса:
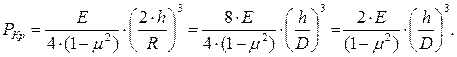 (6.6)
(6.6)
Допускаемое рабочее давление определяется при введении в формулу Бресса коэффициента запаса устойчивости оболочки (m):
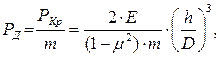 (6.7)
(6.7)
где m = 2,6 – коэффициент запаса устойчивости по ГОСТ 14249-88.
Если также принять значение коэффициента Пуассона m = 0,3 (для сталей), то после подстановки в уравнение (6.7) получим уравнение допускаемого рабочего давления инженерного вида:
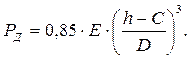 (6.8)
(6.8)
При условии, если задано рабочее давление, то толщина оболочки (h) может быть определена из уравнения (6.8):
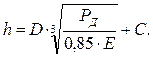 (6.9)
(6.9)
Полученные формулы применимы, если эквивалентные напряжения (sЭКВ) не превышают значений допускаемых напряжений, определяемых как меньшая величина из двух видов значений:
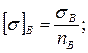
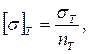
где nВ и nТ – коэффициенты запаса по временному пределу прочности и пределу текучести.
По теории наибольших касательных напряжений ответственность за разрушения несут эквивалентные напряжения, которые определяют по формуле:
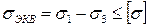 , (6.10)
, (6.10)
где 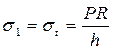 – тангенциальные напряжения;
– тангенциальные напряжения;
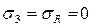 – радиальные напряжения.
– радиальные напряжения.
P – расчетное давление, МПа;
R– определяющий геометрический размер оболочки (радиус), м;
h – толщина оболочки, м;
Если это условие не выполняется, то тогда расчет выполняют по формуле:
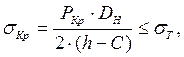 (6.11)
(6.11)
где РКр = РД · nуст – критическое давление; (6.12)
nуст – коэффициент запаса устойчивости, определяемый по формуле:
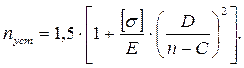 (6.13)
(6.13)
Подставляя значения (6.12) и (6.13) в уравнение (6.11) и решая его относительно допускаемого давления (РД), получим:
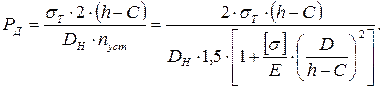 (6.14)
(6.14)
Умножая выражение (6.14) на дробь Е/Е, получим формулу Соусвелла:
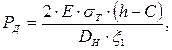 (6.15)
(6.15)
где 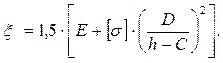 (6.16)
(6.16)
Расчет на устойчивость коротких оболочектакже как и длинных, сводится к определению критического и допускаемого рабочего давления. К категории коротких относят оболочки, для которых знак неравенства в выражении (6.2) меняется на противоположный.
У коротких оболочек сильное влияние оказывает заделка края, поэтому формулы расчета длинных оболочек для них не применимы. В общем виде уравнение прочности (критического давления) имеет вид:
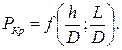 (6.17)
(6.17)
В теории расчета и проектирования коротких оболочек наибольшее применение находит уравнение Мизиса:
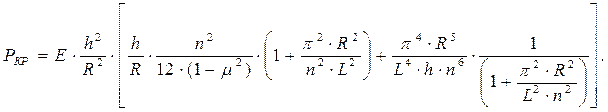
(6.18)
Так как (Ркр) зависит от числа волн (n), то по результатам экспериментальных исследований строится график, структура которого представлена на рисунке 6.3.

Рисунок 6.3 – Зависимость критического давления от числа волн смятия
Для приближенных практических расчетов критическое число волн смятия можно определить по формуле:
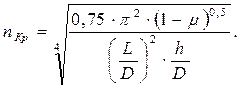 (6.19)
(6.19)
Для большинства оболочек, у которых (L > R) отношение:
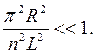
Тогда последний сомножитель в уравнении (6.18) можно принять равным 1 и расчетное уравнение критического давления упростится, принимая вид:
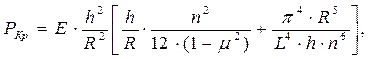 (6.20)
(6.20)
откуда 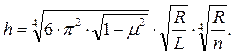 (6.21)
(6.21)
Принимая m = 0,3, получим расчетную формулу критического давления:
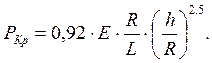 (6.22)
(6.22)
Подставляя в уравнение (6.20) значение коэффициента запаса устойчивости (m = 2,6) и число волн смятия (n = 2), получим итоговые расчетные формулы:
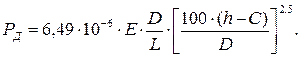 (6.23)
(6.23)
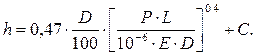 (6.24)
(6.24)
Дата добавления: 2016-06-13; просмотров: 938;
