Метод наименьших квадратов.
При использовании графического метода берутся все данные за исследуемый период, все точки наносятся на график и заполняется корреляционное поле. Затем визуально проводится линия совокупных затрат, которая пересекаясь с осью ординат, показывает величину общих издержек в общей сумме затрат [6,24].
На практике очень часто пользуются более простым методом разделения затрат на постоянные и переменные — методом высшей и низшей точек. Его сущность заключается в том, что изучаются данные за определенное время, в котором выделяются периоды с максимальным и минимальным объемами производства, и определяется отклонение в объемах производства (∆Х) по формуле:
∆Х = Xmax — Хmin, ( 1.3)
где Xmax, Xmin — объем производства соответственно в
максимальной и минимальной точках.
Затем рассчитывается отклонение в затратах (∆3) на производство в тех же периодах (максимального и минимального объемов производства) по формуле:
∆3 = 3max — 3min, (1.4)
где Зmах, Зmin— затраты соответственно в максимальной
и минимальной точках.
Рассчитав данные величины, можно определить ставку переменных затрат на единицу продукции С:
С = ∆3 : ∆Х. ( 1.5)
Зная ставку переменных расходов на единицу продукции, объем производства (максимальный или минимальный) и совокупные затраты в исследуемом периоде, можно найтиусредненное значение постоянных затрат в данном периоде:
а = Y- bХ, (1.6)
где а — постоянные затраты в определенный
промежуток времени;
Y — совокупные затраты в исследуемом периоде;
b — переменные затраты на единицу продукции
(ставка переменных расходов на единицу
продукции);
X — объем производства в исследуемом периоде.
Подставляя рассчитанные значения постоянных, переменных затрат и разные значения объема производства в формулу (1.2), можно получать информацию о предполагаемом размере совокупных затрат, которые должно произвести предприятие, чтобы выпустить запланированный объем продукции. На основе этой же формулы можно построить график зависимости совокупных затрат от объема производства, что позволит более наглядно представить перспективы производства. Особенность построенного графика состоит в том, что он пересекает ось, показывающую изменение затрат, в точке, соответствующей значению постоянных затрат. Но не следует забывать, что, используя в исходных расчетах изменения объемов производства и затрат, мы получим приблизительные данные о совокупных затратах.
При разделении затрат на постоянные и переменные нужно помнить, что переменные затраты изменяются пропорционально уровню деловой активности. Значит, увеличение объема производства в несколько раз повлечет за собой увеличение размера переменных затрат в такое же количество раз. Но важно понимать и то, что совокупные переменные затраты зависят от объема производства, а переменные затраты на единицу продукции — это постоянная величина [24].
Пример
Рассмотрим метод «мини-макси», используя следующие данные.
Таблица 1.2
| Показатель | Объем, шт. | Затраты, руб. |
| Максимальное значение | ||
| Минимальное значение | ||
| Разность |
Переменные затраты на единицу = Разность затрат / Разность объемов продукции » 3,14 руб.
Определив, что переменные затраты составляют 3,14 руб. на единицу, мы можем определить величину постоянных затрат. Для этого используем исходные данные о максимальном или минимальном объемах производства. Постоянные затраты а рассчитываются вычитанием переменных затрат при соответствующем объеме из общей суммы затрат.
512 =а +3,14 х 24;
а = 512 - 3,14 х 24 = 512 - 75,36 = 436,64 » 437.
Отсюда формула затрат для нашего примера:
Y= 437 + 3,14Х
Заметим, что формула вычисления затрат по методу «мини-макси» справедлива только в области релевантности (область релевантности — диапазон, в пределах которого сохраняется определенная модель поведения затрат) и может не дать нужных результатов вне этой области. Метод «мини-макси» прост в применении, но его недостаток заключается в том, что для определения затрат используются только две точки. В общем же случае двух точек недостаточно для определения зависимости и расчета сумм затрат. В частности, периоды, в которых объем производства был необычайно низким или высоким вследствие различных причин (отсутствия сырья, простоя оборудования, поломки, т.е. случайные точки), могут исказить общую картину, поэтому для более точного расчета величины затрат используют методы, основанные на большом количестве наблюдений за поведением затрат.
Для установления зависимости между затратами и объемом производства и определения суммы затрат используют методы математической статистики, в частности метод наименьших квадратов (МНК). Дифференциация затрат с помощью МНК дает наиболее; точные результаты. Согласно этому методу прямая затрат строится таким образом, чтобы сумма квадратов отклонений расстояний от всех точек до теоретической линии регрессии была бы минимальной. Функция Y = a + bХ, отражающая связь между зависимой и независимой переменными, называется уравнением регрессии, а и b — параметры уравнения.
Применительно к задачам управления затратами функция Y в этом уравнении - зависимая переменная (общая сумма затрат, смешанные затраты); а - общая сумма постоянных затрат; b - переменные затраты на единицу продукции; X - независимая переменная (объем производства).
Математический аппарат МНК описан достаточно подробно в специальной литературе. Итак, сумма квадратов отклонений фактических значений функции Y от значений, найденных по уравнению регрессии, должна быть наименьшей:
å( Yф — Yi) => min, ( 1.7)
где Уф — фактические значения;
Yi — расчетные значения, вычисляемые по заданной
формуле.
Это условие приводит к системе нормальных уравнений, решение которых позволяет определить параметры уравнения регрессии. Эти уравнения имеют вид:
åху = aåx + båx2;
åу = åа + båх, (1.8)
где х — объем производства;
у — совокупные затраты;
п — количество наблюдений.
Алгоритм решения следующий.
Шаг 1. Рассчитываются åx; åy; åxy; åx2 и п.
Шаг 2. Рассчитанные величины подставляются в уравнения.
Шаг 3. Система уравнений решается относительно одного из параметров, обычно параметра b, т.е. переменных затрат на единицу продукции.
Шаг 4. Зная один из параметров, находим другой, т.е. а или постоянные затраты [24].
По степени управляемостизатраты делятся на релевантные и нерелевантные.
Релевантные затраты – затраты, отличающие одну альтернативу от другой, т.е. которые изменяются в результате принятия управленческого решения. Они учитываются при принятии решений.
Нерелевантные затраты – это затраты, которые от принятого решения не зависят.
Бухгалтер-аналитик, представляя руководству предприятия исходную информацию для выбора оптимального решения, готовит свои отчеты таким образом, чтобы они содержали только релевантную информацию ( рис. 1.4).
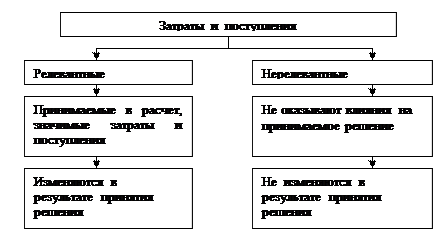
Рис. 1.4 Разделение затрат на релевантные и нерелевантные
Область релевантности – это диапазон, в пределах которого сохранятся определенная модель поведения затрат
Пример
Предприятием А, реализующим продукцию на внешнем рынке, впрок были закуплены основные материалы на сумму 500 руб. Впоследствии в связи с изменением технологии выяснилось, что для собственного производства эти материалы малопригодны. Произведенная из них продукция окажется неконкурентоспособной на внешнем рынке. Однако российский партнер готов купить у данного предприятия продукцию, изготовленную из этих материалов, за 800 руб. При этом дополнительные затраты предприятия А по изготовлению продукции составят 600 руб. Целесообразно ли принимать подобный заказ?
В данном случае сравниваются между собой две альтернативы: не принимать или принимать заказ.
Истекшие затраты по приобретению материалов в сумме 500 руб. уже состоялись и не зависят оттого, какой вариант будет выбран. Они не влияют на выбор решения, не являются релевантными и потому могут не учитываться при принятии решения. Сравним альтернативы по релевантным показателям (табл. 1.3).
Таблица 1.3
|
Видно, что, выбрав альтернативу II, предприятие А уменьшит свой убыток от покупки ненужных ему материалов на 200 руб., сократив его с 500 до 300 руб.
Безвозвратные затраты – это затраты, которые возникли в результате принятого ранее решения и которые не могут быть изменены никаким решением в будущем.Это истекшие затраты, которые не могут быть изменены никакими управленческими решениями.
Из предыдущего примера видно, что 500 руб. - безвозвратные затраты. Безвозвратные затраты не учитываются при принятии решений.
Однако не всегда не принимаемые в расчет при оценках затраты являются безвозвратными. Так, в результате двух альтернативных методов производства может оказаться, что суммы затрат на основные материалы одинаковы для обоих методов, т.е. при выборе варианта затраты на основные материалы можно отнести к категории нерелевантных. Но они не безвозвратные, поскольку будут отнесены ( или не будут понесены, если мы отклоним решение) только в дальнейшем.
Вмененные (воображаемые) затраты в результате принятого альтернативного решения характеризуют возможность, которая потеряна или которой жертвуют, в результате выбора.
По существу это упущенная выгода предприятия.
Пример.
Печь хлебопекарни работает на полную мощность в три смены и за неделю выпускает батонов нарезных на 10 тыс. руб. Оптовый покупатель предлагает пекарне новый недельный заказ по выпечке сдобы, что повлечет за собой дополнительные переменные затраты на сумму 3 тыс. руб. Какой должна быть минимальная цена договора?
Приняв заказ, пекарня откажется от дохода в 10 тыс. руб., получаемого ранее от выпечки батонов, т.е. по существу понесет убытки на 10 тыс. руб. Эту сумму предприятию необходимо учесть при обсуждении условий договора. Цена договора не может опуститься ниже 13 тыс. руб. (10 + 3). При этом 10 тыс. руб. — вмененные (воображаемые) затраты, или упущенная выгода предприятия.
Необходимо иметь в виду, что данная категория затрат применима лишь в случае ограниченности ресурсов, в приведенном примере - при полной загрузке производственных мощностей. Если бы хлебопекарная печь была недогружена и работала с простоями, о вмененных затратах речь бы не шла.
Дата добавления: 2016-06-13; просмотров: 3722;
