Количественная оценка степени риска
Для оценки экономической эффективности конкретных инновационных проектов и принятия решения о выборе оптимального варианта необходима количественная оценка степени риска. Базовыми предпосылками осуществления количественных оценок уровня рискованности инновационных проектов, по мнению многих исследователей, выступают следующие положения:
· Ход реализации каждой конкретной инновационной разработки и ее результат однозначно непредсказуемы. Вместе с тем, существуют объективные закономерности, определяющие общие тенденции хода реализации инновационных разработок и вероятностные характеристики получаемых результатов. Проявление этих закономерностей подтверждается статистическими наблюдениями за инновационной деятельностью.
· Статистика инновационных процессов подчиняется общим правилам математической статистики.
· Важнейшими характеристиками риска выступают два параметра: вероятность возникновения в ходе инновационной деятельности неблагоприятной (рисковой) ситуации и количественная оценка уровня возможных потерь.
Основываясь на этих базовых положениях, формализованное описание риска инновационной деятельности можно представить в форме функциональной зависимости следующего вида:
| R=F(p,u), | (2.18) |
где p – вероятность возникновения неблагоприятной ситуации в ходе реализации нововведения; u - количественная оценка уровня возможных потерь.
Если в ходе анализа установлено, что возможны несколько результатов инновации, каждый из которых неодинаково оценивается инноватором (самый удачный, удачный, абсолютно неудачный), то подобные инновации называются рисковыми. Для них в первую очередь оценивается параметр наиболее реального результата (re), определяемый по формуле математического ожидания:
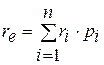 , ,
| (2.19) |
где ri – оценка i-го возможного результата инновационной разработки; pi – вероятность получения i-го результата; n – число возможных результатов.
Количественной оценкой риска той или иной инновационной разработки принято считать вариацию (var) – т.е. разброс возможных результатов инновационной операции относительно ожидаемого значения (математического ожидания):
 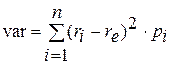 . .
| (2.20) |
Помимо этого, для оценки уровня риска могут быть использованы показатели среднего отклонения (s) – дисперсии и показатель относительного линейного отклонения:
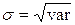 . .
| (2.21) |
Относительное линейное отклонение оценивается с помощью показателя колеблемости (g):
  . .
| (2.22) |
Чем выше оценки всех этих параметров, тем более рискованной считается инновация.
Инновационная деятельность характеризуется одновременным действием нескольких различных тенденций, соответственно порождающих несколько различных видов риска. Поэтому, при проведении обобщенной оценки рискованности инновационного проекта следует опираться на следующие правила:
1. Правило поглощения рисков. Если риски относятся к одной области деятельности и/или их мера совпадает, но проявления негативных факторов происходят независимо друг от друга, то обобщенная вероятность их появления оценивается по максимальному значению вероятностей частных видов риска:
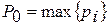 . .
| (2.23) |
2. Правило математического сложения рисков. Если риски относятся к разным областям деятельности и/или их меры различаются, но проявление негативных факторов происходит независимо друг от друга, то обобщенная вероятность их появления оценивается по правилам теории вероятности как оценка суммы вероятностей независимых событий:
| P0=P1+P2+P1.P2 . | (2.24) |
3. Правило логического сложения рисков. Если риски относятся к различным областям деятельности, а негативные факторы проявляются в зависимости один от другого, то обобщенная вероятность их появления оценивается на основе правила логического сложения – степень риска в данном случае рассчитывается как сумма произведений риска одного события на шансы (вероятность появления) других:
 , ,
| (2.25) |
где Pi- степень риска для i-го случая; qj- оценка шанса для j-го случая (qj=1-Pi);
Итоги большого количества проведенных статистических исследований позволяют сделать вывод о том, что распределение результатов инноваций в большинстве случаев имеет характер нормального распределения. Нормальное распределение (распределение Гаусса) представляет собой вид распределения случайных величин, с достаточной точностью описывающий распределение плотности вероятности результатов производственно-хозяйственной, финансовой, инновационной деятельности или изменений условий внешней среды, поскольку показатели, характеризующие их, определяются большим числом независимых случайных величин, каждая из которых в отдельности относительно других играет незначительную роль и непредсказуема. Применение нормального распределения для оценки рисков инновационной деятельности также связано с тем, что в качестве исходных данных используются, как правило, ряды дискретных значений. Эти теоретические предпосылки, а также результаты апробации различных моделей анализа рисков на основе нормального распределения доказывают адекватность этого теоретического инструмента реальным характеристикам инновационных процессов. Оценка вероятностных характеристик с помощью инструментария нормального распределение базируется на определении величины плотности вероятности распределения некой случайной величины «x», представляемой в следующем виде:
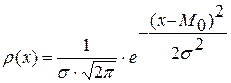 , ,
| (2.26) |
где r(x) – плотность вероятности распределения случайной величины «х»; s - дисперсия (рассеивание) случайной величины «х»; М0 – математическое ожидание величины «х».
Нормальное распределение позволяет количественно оценить вероятность неблагоприятного значения исследуемой величины (вероятность того, что значение случайной величины «x» окажется меньше некого порогового значения x’):
 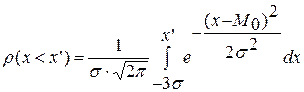 , ,
| (2.27) |
Поскольку основными параметрами нормального распределения являются математическое ожидание и дисперсия, то очевидно, что любое их соотношение поддается нормированию. Это означает, что в расчетах вероятности получения определенных значений оцениваемых характеристик, существует возможность применения таблиц стандартизированного нормального распределения. На практике именно такие таблицы в большинстве случаев и выступают в качестве базы оценок.
При оценках эффективности конкретных инвестиционных проектов применение вероятностных оценок свершения определенных событий может основываться на расчетах вероятностей с использованием ß - распределения. В этом случае экспертным путем задаются возможные значения благоприятного, неблагоприятного и наиболее вероятного результатов: Хблаг, Хнеблаг, Хвероят. Математическое ожидание величины результата в этом случае определяется следующим образом:
 . .
| (2.28) |
Далее становится возможным определить соответствующую оценку дисперсии, и с помощью формулы (8.4.10) оценить вероятность достижения полученного значения переменной Х.
Также на практике широко используется такой инструмент, как Z-статистика. При анализе результатов инновационной деятельности с помощью данного инструмента, используются статистические таблицы стандартного нормального распределения, по которым, исходя из значения коэффициента Z, оценивается вероятность того, что результат инновации окажется не хуже некоего критического уровня, определяемого инноватором или инвестором:
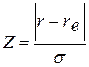 , ,
| (2.29) |
где r – критический уровень результата инновации; rе – наиболее ожидаемый результат инновации.
По значению Z на основе табличных значений оценивается вероятность риска для случаев, когда критический уровень результата превосходит (если инноватор заинтересован в максимизации результата), либо меньше ожидаемого значения (если инноватор заинтересован в минимизации результата).
Вероятность того, что результат нововведения будет иметь качественный уровень хуже ожидаемого, оценивается по следующей формуле:
| P=1-p , | (2.30) |
где p- значение вероятности, полученное по таблице.
Для расчетов экономической эффективности инновационных проектов и принятия решения о выборе оптимального может быть использован коэффициент риска, отражающий соотношение темпов прироста предполагаемых доходов по анализируемому проекту и темпов прироста величины возможных потерь.
Дата добавления: 2016-06-13; просмотров: 910;
