СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ И ЕЕ СВОЙСТВА
Наиболее распространенным видом средних являете средняя арифметическая. Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности являете суммой значений признаков отдельных ее единиц. Для общественных явлений характерна аддитивность (суммарность) объемов варьирующего признака, этим определяется область применения средней арифметической и объясняется ее распространенность как обобщающего показателя. Так, например, общий фонд заработной платы — это сумма заработных плат всех работников, валовый сбор урожая - сумма произведенной продукции со всей посевной площади.
Под средней арифметической понимается такое среднее значение признака, при замене которым индивидуальных значений признака суммарный объем этого признака по совокупности в целом сохраняется неизменным, т.е, средняя арифметическая есть среднее слагаемое.
Она применяется для усреднения абсолютных и относительных величин. Кроме того, средняя арифметическая используется в тех случаях, когда расчет осуществляется по сгруппированным данным или вариационным рядам. В этом случае применяется средняя арифметическая взвешенная:
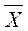 =
= 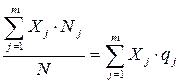 ,
,
где 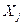 - значение признакав j-ой группе (j=1;m);
- значение признакав j-ой группе (j=1;m);
m – число групп;
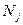 - частота (численность) j-й группы;
- частота (численность) j-й группы;
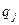 - частость (доля) j-й группы.
- частость (доля) j-й группы.
Если значение признака в группе задано интервалом, то в качестве варианта X 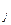 берется середина интервала (центральное значение):
берется середина интервала (центральное значение):
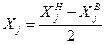 .
.
При этом значение средней будет приближенным.
Средняя арифметическая взвешенная используется также при вычислении средней по групповым средним или по средним отдельных частей совокупности. При этом групповые (частные) средние — 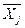 принимаются как варианты, а численности групп — как веса усреднения:
принимаются как варианты, а численности групп — как веса усреднения:
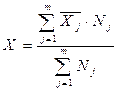 .
.
Средняя арифметическая обладает рядом свойств.
Сущностные свойства средней арифметической:
1)средняя арифметическая постоянной величины равна этой постоянной: А — А, при А = const;
2)алгебраическая сумма линейных отклонений (разностей) индивидуальных значений признака от средней арифметической равна нулю:
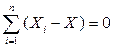 для первичного ряда и
для первичного ряда и 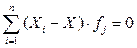 ,
,
где 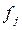 — веса усреднения для сгруппированного ряда. Логически это означает, что все отклонения от средней в ту и другую сторону (положительные и отрицательные), обусловленные случайными причинами, взаимно погашаются;
— веса усреднения для сгруппированного ряда. Логически это означает, что все отклонения от средней в ту и другую сторону (положительные и отрицательные), обусловленные случайными причинами, взаимно погашаются;
3) сумма квадратов отклонений индивидуальных значений признака от средней арифметической есть величина минимальная:
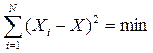
или
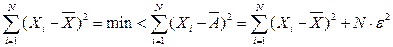 ,
,
где А =  ,(где
,(где  — сколь угодно малая величина), что означает: сумма квадратов отклонений индивидуальных значений признака каждой единицы совокупности от средней арифметической всегда меньше суммы квадратов отклонений вариантов признака от любого значения А, сколь угодно мало отличающегося от
— сколь угодно малая величина), что означает: сумма квадратов отклонений индивидуальных значений признака каждой единицы совокупности от средней арифметической всегда меньше суммы квадратов отклонений вариантов признака от любого значения А, сколь угодно мало отличающегося от 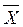 . Такой же вывод получаем для сгруппированных данных.
. Такой же вывод получаем для сгруппированных данных.
Вычислительные свойства средней арифметической:
1) если все значения признака уменьшить (увеличить) на одну и ту же величину А, то и средняя арифметическая уменьшится (увеличится) на ту же самую величину А;
2)если все значения признака разделить (умножить) на какое-либо постоянное число А, то средняя арифметическая уменьшится (увеличится) в А раз;
3)если вес каждого значения признака разделить на какое-либо постоянное число А, то средняя арифметическая не изменится.
Дата добавления: 2016-06-02; просмотров: 1479;
