СУЩНОСТЬ И ЗАДАЧИ ВЫБОРОЧНОГО НАБЛЮДЕНИЯ

Выборочное статистическое исследование — это обследование выборочной совокупности с целью получения достоверных суждений о характеристиках или параметрах генеральной совокупности — θ^Г.

Генеральная совокупность — это полная совокупность единиц (статистическая совокупность).

Выборочная совокупность (выборка) — это часть единиц генеральной совокупности, отобранная в соответствии с принципами выборочного метода. Принципы выборочного метода:

1) обеспечение случайности отбора единиц совокупности (т.е. равной возможности попадания единицы в выборку);

2) обеспечение достаточного числа единиц в выборке.

Условия, требующие проведения выборочного исследования:

• экономия времени и средств в результате сокращения объема работы (при выборочном методе обследованию подвергается 5-10%, реже до 15-20% изучаемой совокупности);

• сведение к минимуму порчи или уничтожения исследуемых объектов (например, при определении прочности пряжи на разрыв нити, при испытании электрических лампочек на продолжительность горения, при проверке консервов на доброкачественность);

• исследуемая совокупность может быть полностью недоступна;

• исследуемая совокупность может не иметь конечного объема.

Чаще всего с помощью выборочного метода исследуются следующие характеристики совокупности:

• среднее арифметическое значение признака в совокупности ( );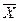

• доля альтернативного признака ( 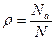),где ρ — доля альтернативного признака в генеральной совокупности;

N_a — число единиц, обладающих заданным значением альтернативного признака в генеральной совокупности;

N — объем генеральной совокупности.

Альтернативный признак — это признак, принимающий два значения. Если одно из этих значений принять как заданное, то доля альтернативного признака будет характеризовать долю (удельный вес) единиц в статистической совокупности, которые имеют заданное значение альтернативного признака. Например, доля нестандартных изделий во всей партии товара, удельный вес продукции собственного производства в товарообороте предприятия, удельный вес продавцов в общей численности работников магазина и т.п.;

• дисперсия признака в совокупности (σ²).

Часто с помощью выборочного метода исследуются не просто характеристики генеральной совокупности, а параметры распределения изучаемого признака генеральной совокупности, если удалось установить (из теоретических соображений), какое именно распределение имеет признак. Например, если заранее известно, что изучаемый признак распределен нормально, то исследуемыми параметрами будут: а — математическое ожидание и σ — среднее квадратическое отклонение. Если же есть основания считать, что признак имеет распределение Пуассона, то необходимо оценить параметр λ— лямбда, которым это распределение определяется.

По данным выборки мы не можем найти точное значение характеристики или параметра генеральной совокупности (θ^Г), однако мы можем получить его приближенное значение (оценку).