Тема 2. Линейное программирование как инструмент принятия управленческих решений

1. Сущность, особенности и потенциальные возможности линейного программирования.

2. Задачи, методы и практические приложения линейного программирования.

Линейное программирование (ЛП) нашло наибольшее распространение в экономике при принятии оптимальных решений, что объясняется следующим:

· математические модели большого числа экономических задач линейны относительно определенных переменных;

· задачи та кого типа наиболее распространены и изучены;

· некоторые задачи, которые не являются линейными, после некоторых преобразований могут быть сведены к задачам линейного программирования;

· много задач ЛП, реализованных на ПК, находят применение в экономической практике.

Любая оптимизационная экономика – математическая модель ЛП включает в себя 3 составных части:

1) целевую функцию, оптимум который необходимо найти;

2) ограничения на переменные в виде линейной системы неравенств (уравнений);

3) условия неотрицательности переменных.

Математическая модель общей задачи ЛП формируется таким образом: необходимо найти максимум или минимум целевой функции

Z=p₁x₁+p₂x₂+…p_nx_n max(min), (1)

при наличии ограничений в виде системы неравенств или (и) уравнений

a₁₁x₁+a₁₂x₂+…a_inx_n (≥, ≤, =) b_i (i=1…M), (2)

и условий неотрицательности переменных

x_j ≥ 0 (j=1…n) (3)

В приведенных формулах 1-3 обозначено:

p_j, a_ij, b_i (i = 1…M, j = 1…n) – известные постоянные коэффициенты; x_j – переменные, которые подлежат определению; значок (≥, ≤, =) показывает, что может использоваться тот или иной вид ограничения неравенств или равенств.

Линейное программирование адекватно прежде всего задачам распределения ресурсов.

2. Примеры задач линейного программирования – задача планирования объема и ассортимента выпускаемой продукции с учетом запасов ресурсов (по видам), задачам составления рациона (задача о диете, задача о смесях), задача о загрузке оборудования, задача о раскрое материалов, транспортная задача.

Методы решения задач ЛП – геометрический метод; симплексный метод. Для реализации симплексного метода – последовательного улучшения решения – необходимо освоить три основных элемента:

· способ определения какого-либо первоначального допустимого базисного решения задачи;

· правило перехода к лучшему (точнее, не худшему) решению;

· критерий проверки оптимальности найденного решения.

Для использования симплексного метода задача линейного программирования должна быть приведена к каноническому виду, т.е. система ограничений должна быть представлена в виде уравнений.

Каждой задаче ЛП соответствует другая задача, называемая двойственной, или сопряженной, по отношению к исходной.

Исходная задача – составить такой план выпуска продукции x = (x_1…x_n), при котором прибыль (выручка) от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов.

F = c₁x₁ + c₂x₂ + … c_nx_n à max (4)

при ограничениях:

a₁₁x₁+a₁₂x₂+…a_1nx_n ≤ b₁

a₂₁x₁+a₂₂x₂+…a_2nx_n ≤ b₂ (5)

…………………………

a_m1x₁+a_m2x₂+…a_mnx_n ≤ b_M,

и условии неотрицательности

x₁ ≥ 0, x₂ ≥ 0,… x_n ≥ 0, (6)

где с_j – прибыль (выручка) от реализации единицы продукции p_j (или цена продукции p_j)

a_ij – число единиц ресурса s_i, потребляемого при производстве единицы продукции p_j

j = 1,2…n; i = 1,2…M

n – число видов продукции;

M - число видов ресурсов;

x_j – план выпуска продукции p_j;

b_i – запас ресурса s_i.

Обратная задача – найти такой набор цен (оценок) ресурсов У = (у_1,у_2…у_n) при которых общие затраты на ресурсы (создание запаса ресурсов) будут минимальными при условии, что затраты на ресурсы при производстве единицы продукции каждого вида будут отклоняться от цены продукции в меньшую сторону не более чем в k раз.

k – коэффициент, определяемый исходя из нормативной рентабельности продукции.

k = 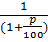, (7)

где р - нормативный процент рентабельности продукции

z = b₁y₁+b₂y₂+…b_My_M à min (8)

при ограничениях

a₁₁y₁+a₂₁y₂+…a_M1y₁ ≤ k×c₁,

a₁₂y₁+a₂₂y₂+…a_m2y₁ ≤ k×c₂, (9)

…………………………….

a_1ny₁+a_2ny₂+….a_Mny_M ≤ k×c_n

и условии неотрицательности

y₁≥0, y₂≥0,… y_n≥0, (10)

При формулировке обратной задачи учитывается и интерес продавца ресурсов.

Цены ресурсов y₁…y_M в экономической литературе получили название учетных, неявных, теневых. Смысл этих названий состоит в том, что это условные «ненастоящие» цены. В отличии от «внешних» цен с₁, с₂… с_n на продукцию, известных, как правило, до начала производства, цены ресурсов y₁…y_M являются внутренними, т.к. они задаются не извне, а определяются непосредственно в результате решения задачи, поэтому их чаще называют оценками ресурсов.

Таким образом, обратная задача – задача минимизации цен на ресурсы.

Компоненты оптимального решения двойственной задачи называются оптимальными (двойственными) сценками исходной задачи. Академик Л.В. Канторович назвал их объективно обусловленными оценками. Объективно обусловленные оценки – условные цены ресурсов. В модели – Л.В. Канторовича рассматриваются возможности превышения затрат над ценой на продукцию. Если ресурсы по оптимальному плану полностью использованы, то объективно обусловленные оценки этих ресурсов ненулевые. Если ресурсы не полностью используются, то объективно обусловленные оценки этих ресурсов нулевые. Объективно обусловленные оценки ресурсов определяют степень дефицитности ресурсов: по оптимальному плану производства дефицитные (т.е. полностью используемые) ресурсы получают ненулевые оценки, а недефицитные – нулевые оценки.

По оптимальному плану в исходной задачи следует производить, например, оба вида продукции ( 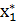=6, 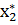=4) при равенстве затрат на ресурсы и цены реализации единицы продукции ( 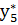=0; 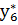=0). Если бы затраты на ресурсы превышали цену изготавливаемой продукции, например, р₂, т.е. 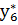>0, то 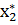=0, и в этом случае производить продукцию p₂ не следовало бы.

Итак, в оптимальный план производства могут попасть только рентабельные, неубыточные виды продукции. Правда, критерий рентабельности здесь своеобразный: цена продукции не превышает затраты на потребляемые при ее изготовлении ресурсы, а в точности равна им. План производства 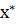= ( 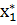, , 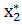… 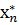) и набор цен (оценка) ресурсов 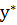= ( 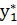, , 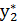… 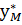) оказываются оптимальными тогда и только тогда, когда выручка от продукции, найденная при «внешних» (известных заранее ценах) с₁…с_n равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам (оценкам) y₁…y_M.