Шекті қабаттың негізгі теориялары
Жылуөткізгіштік туралы негізгі ұғымдар.Фурье заңы.Шектік жағдайлар туралы ұғым.
Жылу өткізгіштік негізгі заңдарына Фурье заңы жатады. Бұл заң жылу мөлшері уақыт ішінде температураның төмендеуіне пропорциональ және қима ауданымен жылудың таралуына перпендикуляр бағытта жүреді:
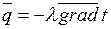 ,
,
мұндағы 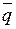 - жылу ағынының тығыздығы, Вт/м2;
- жылу ағынының тығыздығы, Вт/м2; 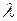 - коэффициент.
- коэффициент.
« - » белгісі, жылу ағысының бағыты мен температура градиенті қарама қарсылығын көрсетеді.
λ коэффициенті жылу өткізгіштік коэффициенті деп аталады. Ол заттың физикалық қасиеті болып табылады және оның жылу өткізу қабілетін сипаттайды. Жылу өткізгіштік коэффициентінің мәні, to = 1oC grad изотермиялық бет бірлігі арқылы уақыт бірлігінде өтетін жылу мөлшерін білдіреді.
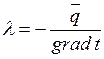 , [Вт/м·Со]
, [Вт/м·Со]
λ коэффициент мәні көптеген фактордан тәуелді: материал табиғаты, оның құрылымынан, тығыздығынан, ылғалдылық, қоспаның болуынан, қысым, температурадан және т.б.
температурадан тәуелділік:
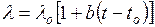 ,
,
мұндағы 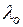 - tо жылу өткізгіштік коэффициенті. Әдетте tо = 20оС қабылданады;
- tо жылу өткізгіштік коэффициенті. Әдетте tо = 20оС қабылданады;
t – пайдалану температурасы;
b – материал табиғатына тәуелді коэффициент.
Шекті қабаттың негізгі теориялары
Қажетті есепті шешу үшін дененің температуралық өрісін, формасын және өлшемдерін білу керек. Мұндай мәліметтер процестің шекті жағдайлары деп аталады. Жылу ауысу процесінің шекті жағдайлары үш түрлі әдіспен көрсетіледі:
1 түрді шекті жағдайлар - әр уақытта дененің беттігінде температура өрісі беріледі;
2 түрді шекті жағдайлар - әр уақытта дененің әр нүктесінде жылу ағынының тығыздығы көрсетіледі;
3 түрді шекті жағдайлар – денені қоршаған ортаның температурасы және жылуалмастыру заңы беріледі.
1-түрдегі шекті жағдайдағы және стационарлы режимдегі қабырғаның жылуөткізгіштігі:
1. жалпақ бір қабатты қабырға: 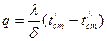 , Вт/м2
, Вт/м2
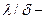 шамасы жылуөткізгіштікі, ал
шамасы жылуөткізгіштікі, ал  кері шама қабырғаның термиялық кедергісі деп аталады.
кері шама қабырғаның термиялық кедергісі деп аталады.
2.жалпақ көп қабатты қабырға: 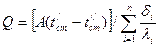 , Вт
, Вт
3. цилиндрлік бір қабатты қабырға:
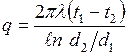 , Вт/м
, Вт/м
4. цилиндрлік көп қабатты қабырға:
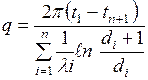 , Вт/м
, Вт/м
5.шар тәрізді қабырға:
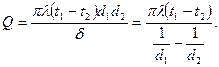 Вт
Вт
III ш.ж. қабырғадағы жылу өткізгіштік. Жылутасмалдау коэффициенті.
1. жалпақ бір қабатты қабырға:
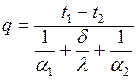 , Вт/м2
, Вт/м2
к= 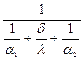 жылу тасмалдау коэффициенті деп аталады, К әріппімен белгіленеді, өлшем бірлігі:
жылу тасмалдау коэффициенті деп аталады, К әріппімен белгіленеді, өлшем бірлігі: 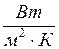 .
.
қабырғаның бірлік беті арқылы уақыт бірлігінде ыстық көзден, суық көзге, олардың арасындағы температура айырмашылығы 1о болғанда өтетін жылу тасмалдау коэффициентінің сандық мәні.
жылу тасмалдау коэффициентіне кері шаманы жалпақ біртекті қабырғаның жалпы термиялық кедергісі деп атайды:
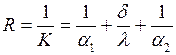 ,
, 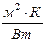
2.жалпақ көп қабатты қабырға:
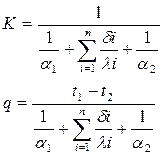
3. цилиндрлік бір қабатты қабырға:
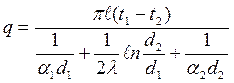 , Вт/м
, Вт/м
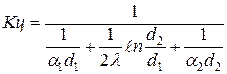 шамасын жылу тасмалдаудың сызықтық коэффициенті деп атайды, өлшем бірлігі
шамасын жылу тасмалдаудың сызықтық коэффициенті деп атайды, өлшем бірлігі 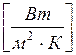 .
.
4.цилиндрлік көп қабатты қабырға:
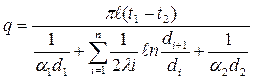 , Вт/м
, Вт/м
5. шар тәрізді қабырға:
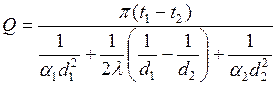 , Вт
, Вт
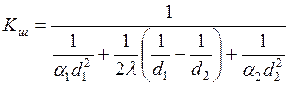 - шарлы қабырғаның жылу тасмалдау коэффициенті деп аталады және
- шарлы қабырғаның жылу тасмалдау коэффициенті деп аталады және 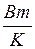 өлшем бірлікке ие болады.
өлшем бірлікке ие болады.
Тақырып Ковективті жылу алмасудың негізгі ұғымдары.Ньютон-Рихман заңы.Ұқсастық теориясы. Ковективті жылу алмасудың ұқсастық теңдеуі
Конвективті жылу алмасу тек қана (газдарда, сұйықтарда) өтеді, бұл кезде жылуды тасымалдау ортаның көлемін тасмалдаумен жүзеге асады. Конвекциямен жылуды тасымалдау әрқашан жылуөткізгіштікпен байланысты. Конвекция мен жылуөткізгіштіктің бірлескен процесін конвекциялық жылуалмасу деп атайды.
Амалсыз (ортаның қозғалысы жасанды туғызылады) және еркін (қозғалыс ортаның суық және қызған көлемдері арасында олардың қызумен және тығыздықтары айырмашылықтарынан пайда болады) конвекцияны ажыратады
Конвекциялық жылу тасмалдаудың негізгі заңы Ньютон-Рихман:
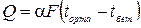
мұндағы 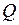 – жылу ағыны, Вт;
– жылу ағыны, Вт;
F – бет ауданы, м2;
tорта – орта температурасы, оС;
tбетв – бет температурасы, оС;
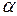 – жылу беру коэффициенті, Вт/м2 · оС.
– жылу беру коэффициенті, Вт/м2 · оС.
α жылу бер коэффициенті орта мен бет арасындағы жылу алмасу ќарќынын сипаттайды және беттің аудан бірлігімен уаќыт бірлігінде орта мен бет арасындағы температуралар айырымасы 10С берілетін жылу мөлшеріне сан жағынан тең. Көптеген факторларға тәуелді:
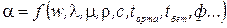
Конвекциялық жылуалмасу толықтай үш дифференциалдық теңдеумен сипатталады:
1) Фурье-Кирхгофтың жылуөткізгіштік теңдеуі, қозғалатын ортаның кез келген нүктесінде кеңістік пен уақыт ішіндегі температуралық өзгерістердің арасындағы байланысты анықтайды: 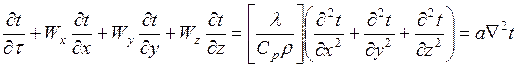 (
(
2). Навье-Стокстың қозғалыс теңдеуі:
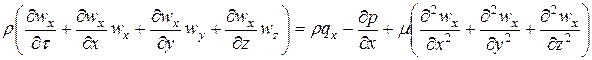
3). Тұтастық пен үздіксіздік теңдеулері: 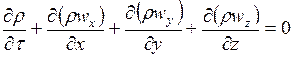
Дата добавления: 2016-06-02; просмотров: 2189;
