Састық теориясы

Ұқсастық туралы ұғым геометрияда пайда болған.Олар бізге белгілі, геометриядағы ұқсас фигуралардың сәйкестілік, өлшемдерінің қатынастары бірдей.

Практикалық жағдайда конвективтік жылуалмастыру коэффиценті кестелер жинақтарынан табылады. Осы себептен практикалық есептерде ұқсастар теориясының негіздерін пайдаланады. Бұл термин геометриядан алынған. (2.1- сурет).

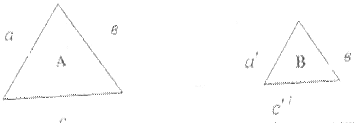
2.1 - сурет

Егер 6-суретте көрсетілген А және В фигураларына келесі шарт орындалатын болса:

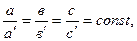
Осы фигулалар бір-біріне ұқсас деп есептеледі.

Физикалық оқиғаға геометриялық көзқарасты келтіретіндей болсақ физикалық ұқсастықты анықтаймыз:

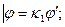
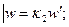
мұнда 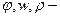бірінші физикалық оқиғаның параметрлері;

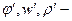екінші физикалық оқиғаның параметрлері;

ұқсастық константалары.

Жылуалмастыру процесінде көрсетілген әдіс бойынша көптеген константалар, өлшемсіз критерилер анықталған.(Рейнольде, Нуссельт, Прандталь т.б). Ұқсастық теориясының негіздерінде үш теорема пайдаланған. Бұл теоремалар физикалық оқиғаны жан-жақты талдауға мүмкіндік туғыздырады.

1 теорема: ұқсас оқиғалардың ұқсастық сандары бір-біріне тең;

2 теорема: Ұқсас оқиғалардың өзара байланысын ұқсастық сандармен көрсетуге болады. Мұндай байланыс ұқсастық теңдеуі деп аталады;

3 теорема: жағдайлары бір-біріне тең оқиғалар өзара ұқсас деп саналады.

Ұқсастық сандарға жататындар:

- Рейнольд саны.Қоршаған ортаның гидромеханикалық сипаттамасы.

Жылуалмастыру процесін анықтауға қажет:

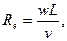
мұндағы ағын жылдамдығы;

-геометриялық параметр;

кинематикалық тұтқырлық.

Бірдей мәндері бар барлық ұқсас процестер үшін құбылысты сипаттайтын шамалардың белгілі кешеннен тұрады. Мұндай мәндерді ұқсастық сандар деп атайды. Өзіне тән белгісі бар ұқсастық саны – оның өлшемсіздігі.

Рейнольд саны.Қоршаған ортаның гидромеханикалық сипаттамасы.

Жылуалмастыру процесін анықтауға қажет:

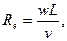
мұндағы ағын жылдамдығы;

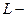геометриялық параметр;

кинематикалық тұтқырлық.

Нуссельт саны –конвекциялық жылуалмасудың қарқынын сипаттайды:

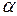– жылу беру коэффициенті;

ℓ – ерекше өлшем;

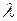– ортаның жылуөткізгіштік коэффициенті.

Грасгоф саны – еркін конвекция кезіндегі көтеру күшінің тиімділігін сипаттайды:

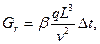
β-көлемдік кеңею коэффициенті;

q – ауырлық күшінің үдеуі;

_Δ t – орта мен бет арасында температура айырмасы;

ℓ – геометриялық параметр.

Прандтль саны – сұйықтың жылу физикалық қасиеттерінің өлшемсіз сипаттамасы:

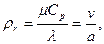
мұндағы ν –кинематикалық м²/с,

μ – динамикалық тұтқырлық Па·с,

с_р –изобарлық массалы жылусыйымдылық Дж/(кг·К)

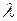– жылуөткізгіштік коэффициенті.

Фурье саны – жылулық гомохрондылық критериясы:

мұндағы τ – уақыт.

а – температураөткізгіштік коэффициенті.

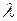– жылуөткізгіштік коэффициенті.

Фруд саны – гравитациялық ұқсастық саны, ағындағы инверсия мен ауырлық күштерінің қатынас шамасын сипаттайды:

Эйлер саны - қысы өрістерінің ұқсастық критериясы:

∆p –сұйық қозғалысы участігіндегі қысымның өзгеруі

Архимед саны – еркін конвекция критериясы:

Вебер(беттік тартылыс):

Био саны (стационарлы емес режимде пайдаланылады).

мұндағы жылу беру коэффициенті,

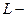геометриялық өлшем;

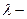дененің жылуөткізгіштік коэффициенті.

- еркін конвекцияның ұқсастық теңдеуі: Nu = f (Gr, Pr);

- амалсыз конвекцияның ұқсастық теңдеуі: Nu = f (Рr, Re);

- еркін-амалсыз конвекция теңдеуі:

Nu = f (Рr, Re, Gr).

Рr, Re және Gr критерияларыанықтауыштар, ал Нуссельт критериясы – анықталатын болып табылады.