Уравнивание нивелирной сети способом последовательных приближений
Рассмотрим нивелирную сеть, изображенную на рисунке 25.2. в соответствии с параметрическим способом уравнивания поправок обозначим искомые отметки:
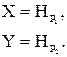
Для измеренных превышений по ходам напишем параметрические уравнения поправок:
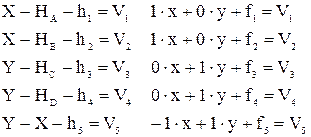
где fi = Hисх + hi – Hокр.
Для решения этой системы уравнений с двумя неизвестными применяем условие [PV2] = min. В методе наименьших квадратов доказывается, что [pav] = 0 и [pbv] = 0, где a и b – коэффициенты при x и y, т.е.:
P1V1 + P2V2 + P5V5 = 0,
P3V3 + P4V4 + P5V5 = 0.
После преобразований получим:
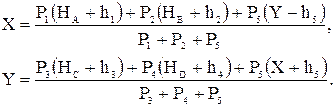
По этим формулам можно найти значения X и Y способом последовательных приближений. При этом в приближения можно взять значения X и Y, найденные от исходных пунктов. Например, для первого приближения вычисления Х берем:
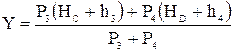
и включаем его в вычисления Х, а полученное значение Х включаем в первое приближение для вычисления Y. Полученное значение y подставляем во второе приближение для вычисления Х и т.д.
Вычислив поправки V, выполняем оценку точности по известным формулам.
Дата добавления: 2016-06-02; просмотров: 2063;
