Уравнение реальных волн
Мы рассмотрели интерференцию волн, описываемых уравнениями вида:
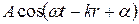 (1)
(1)
Однако такие волны являются математической абстракцией, поскольку волна, описываемая (1), должна быть бесконечной во времени и пространстве. Только в этом случае величины 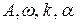 могут быть определенными константами.
могут быть определенными константами.
Реальная волна, образующаяся в результате наложения цугов от различных атомов, содержит в себе составляющие, частоты которых лежат в конечном диапазоне частот 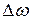 (соответственно волновые векторы в
(соответственно волновые векторы в 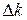 ), а А и a испытывают непрерывные хаотические изменения. Колебания, возбуждаемые в некоторой точке накладывающимися реальными волнами, можно описать выражением:
), а А и a испытывают непрерывные хаотические изменения. Колебания, возбуждаемые в некоторой точке накладывающимися реальными волнами, можно описать выражением:
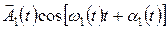
 и
и 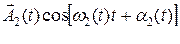 (2)
(2)
Причем хаотические изменения функций от времени в (2) являются независимыми.
Для простоты анализа положим амплитуды волн постоянными и одинаковыми (экспериментально это условие реализуется достаточно просто):
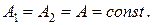
Изменения частоты и фазы можно свести к изменениям только частоты или только фазы. Действительно, допустим, негармоничность функций (2) обусловлена скачками фазы. Но, по доказываемой в математике теореме Фурье, любую негармоническую функцию можно представить в виде суммы гармонических составляющих, частоты которых заключены в некоторых 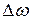 . В предельном случае сумма переходит в интеграл: любая конечная и интегрируемая функция
. В предельном случае сумма переходит в интеграл: любая конечная и интегрируемая функция 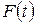 может быть представлена интегралом Фурье:
может быть представлена интегралом Фурье:
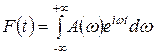 , (3)
, (3)
где 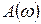 есть амплитуда гармонической составляющей частоты
есть амплитуда гармонической составляющей частоты 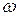 , аналитически определяемая соотношением:
, аналитически определяемая соотношением:
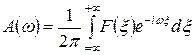 (4)
(4)
Итак, негармоническая вследствие изменения фазы функция представима в виде суперпозиции гармонических составляющих с частотами в некотором 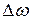 .
.
С другой стороны, функцию с переменной частотой и фазой можно свести к функции с переменной только фазой:
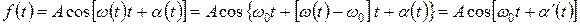 (5)
(5)
Поэтому для укрощения дальнейшего анализа будем считать:
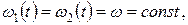
т. е. реализуем фазовый подход к понятию «Временная когерентность».
Дата добавления: 2016-06-02; просмотров: 701;
