Влияние монохроматичности на когерентность
В рамках рассмотренных нами представлений длина когерентности по порядку величины должна равняться длине цуга волны. Однако экспериментально легко установить, что свет с длиной волны, 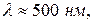 в котором имеются волны, отличающиеся, длиной не более чем на 1 нм, характеризуется временем когерентности
в котором имеются волны, отличающиеся, длиной не более чем на 1 нм, характеризуется временем когерентности 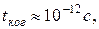 чему соответствует
чему соответствует 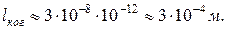
Такое несоответствие наших представлений и эксперимента указывает на то, что мы не учли влияния каких-то очень существенных факторов. Оказывается, что таким фактором является немонохроматичность волны.
Действительно, представление о том, что все атомы тела излучают идентичные цуги волны с постоянной амплитудой, строго определенной частоты 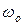 , в течение одинакового времени
, в течение одинакового времени 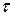 не соответствует действительности по ряду причин:
не соответствует действительности по ряду причин:
1. Энергия электрона в возбужденном состоянии атома не является (принципиально!) строго определенной. Поэтому различные атомы излучают волны различной частоты.
2. Излучающие атомы движутся, и длины их волн различны вследствие эффекта Доплера.
3. Но даже если пренебречь или исключить влияние этих причин, сама конечность времениизлучения атома приведет к тому, что излучение будет состоять не из одной частоты, а будет заключено в конечном диапазоне частот 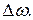
Для объяснения этого фактора рассмотрим идеализированную ситуацию, когда свет состоит из последовательности идентичных цугов с постоянной амплитудой частоты 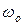 и длительностью
и длительностью 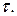 Фаза каждого нового цуга случайна. В такой ситуации время когерентности
Фаза каждого нового цуга случайна. В такой ситуации время когерентности 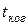 практически идентично длительности цуга
практически идентично длительности цуга 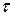 :
:
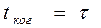
 Каждый цуг описывается функцией
Каждый цуг описывается функцией 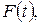 которая отлична от нуля только в течение времени
которая отлична от нуля только в течение времени 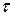 и имеет вид, показанный на графике.
и имеет вид, показанный на графике. 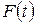 конечна, интегрируема и, согласно теореме Фурье, может быть представлена в виде суперпозиции бесконечного числа гармонических составляющих с амплитудами, зависящими от частоты:
конечна, интегрируема и, согласно теореме Фурье, может быть представлена в виде суперпозиции бесконечного числа гармонических составляющих с амплитудами, зависящими от частоты:
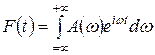 (5)
(5)
 Интенсивность
Интенсивность 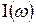 каждой гармонической составляющей пропорциональна квадрату её амплитуды
каждой гармонической составляющей пропорциональна квадрату её амплитуды 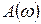 . Для функции
. Для функции 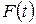 , описывающей, цуг волн частотой
, описывающей, цуг волн частотой 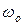 , длительностью
, длительностью 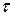 зависимость
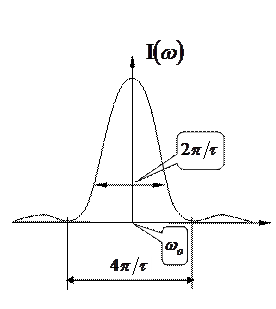
зависимость 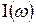 имеет вид, показанный на рисунке. Интенсивность составляющих в частотном интервале
имеет вид, показанный на рисунке. Интенсивность составляющих в частотном интервале
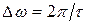 (6)
(6)
намного больше, чем у других. Поэтому 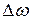 называют эффективным частотным диапазоном Фурье-спектра:
называют эффективным частотным диапазоном Фурье-спектра:
Очевидно, что чем больше 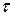 , тем уже максимум на графике, только при
, тем уже максимум на графике, только при 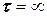 в спектре излучения будет присутствовать одна частота. Именно поэтому гармоническая волна представляет собой математическую абстракцию, поскольку должна быть бесконечной во времени и пространстве.
в спектре излучения будет присутствовать одна частота. Именно поэтому гармоническая волна представляет собой математическую абстракцию, поскольку должна быть бесконечной во времени и пространстве.
Итак, в силу соотношения (6), длительность цуга 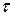 можно связать с эффективным частотным диапазоном фурье-спектра
можно связать с эффективным частотным диапазоном фурье-спектра 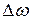 :
:
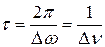 (7)
(7)
Но в нашем случае 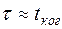 , поэтому
, поэтому
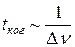 (8)
(8)
и можно считать, что чем шире интервал частот составляющих, присутствующих в данной волне, тем меньше  . Другими словами, в течении
. Другими словами, в течении  немонохроматическую волну приближенно можно считать монохроматической.
немонохроматическую волну приближенно можно считать монохроматической.
Приближенно можно представить себе, что, за время  составляющие с частотами
составляющие с частотами 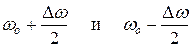 становятся противофазными, т. е. волна перестает быть когерентной самой себе.
становятся противофазными, т. е. волна перестает быть когерентной самой себе.
Очевидно, что если спектр составляющих волны будет расширен не за счет уменьшения длительности, а другим способом, то эффект уменьшения  все равно будет наблюдаться.
все равно будет наблюдаться.
Следовательно, если мы используем не строго монохроматический свет, то длина временной когерентности и время когерентности у него будет намного меньше времени существования цуга и его длины.
Найдем связь 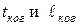 не с частотным интервалом
не с частотным интервалом 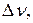 а с диапазоном длин волн
а с диапазоном длин волн 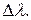 , присутствующих в излучении. Поскольку
, присутствующих в излучении. Поскольку

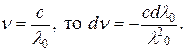

Поэтому конечные 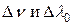 связаны соотношением:
связаны соотношением:
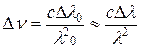 , (9)
, (9)
и время когерентности определяется соотношением:
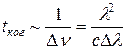 (10)
(10)
Тогда длина временной когерентности определяется соотношением:
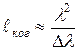 (11)
(11)
Вернемся к примеру, о котором шла речь выше. При 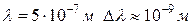 , получаем:
, получаем:
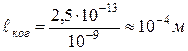 ,
,
в соответствии с экспериментальным значением.
На основе изложенных представлений, можно утверждать, что число полос интерференции, наблюдаемых при наложении частей одной и той же волны, можно связать со степенью монохроматичности света. Действительно, если максимум m-го порядка уже не различим, то это означает, что разность хода достигла длины когерентности:
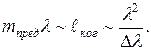

Поэтому
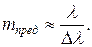
Дата добавления: 2016-06-02; просмотров: 891;
