Природа возникновения ЭДС индукции

Рассмотрим ситуацию, когда ЭДС индукции возникает в контуре, показанном на рисунке при перемещении подвижной стороны контура с некоторой скоро-

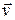стью . Вместе с перемычкой с той же скоростью движутся все электроны внутри нее, и на каждый в магнитном поле действует сила Лоренца, направленная вдоль перемычки:

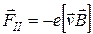
Действие этой силы эквивалентно действию силы со стороны электрического поля с напряженностью

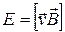. (20.1)

Это поле не имеет электростатической природы, и циркуляция вектора напряженности по контуру дает величину ЭДС, действующей в контуре:

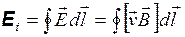. (20.2)

При вычислении интеграла в (20.2) примем за положительное направление обхода контура направление по часовой стрелке. Тогда положительная нормаль к контуру будет направлена так же, как вектор индукции магнитного поля. Элементы в подвижной рамке, в которых собственно действует поле, создающее ЭДС в сумме дают вектор 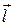. Векторное произведение 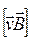является постоянной величиной в пределах подвижной части контура. Поэтому

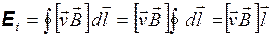. (20.3)

В смешанном произведении векторов в соотношении (20.3) можно провести циклическую перестановку векторов:

. (20.4)

Умножим и разделим это выражение на . Тогда для ЭДС индукции получим:

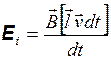. (20.5)

Вектор 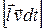по модулю равен площади, описанной подвижной частью за время , однако направлен «к нам». Вектор 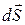направлен по направлению нормали к контуру. Поэтому

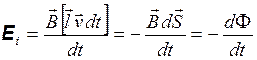. (20.6)

Соотношение (20.7)

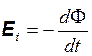. (20.7)

называют обычно законом Фарадея или законом ЭМИ.

Таким образом, в рассматриваемом случае, т.е. при движении проводника в магнитном поле, возникновение ЭДС индукции объясняется действием силы Лоренца на носители заряда в проводнике. В этом объяснении имеется существенный недостаток: индукционный ток проходя по проводникам совершает некоторую работу, а сила Лоренца работы совершать не может.

Это противоречие является кажущимся. Электроны под действием силы Лоренца приходят в движение со скоростью , направленной по вектору 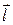. Это движение вызывает появление второй составляющей силы Лоренца 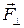, направленной навстречу скорости движения подвижной части контура. Для поддержания движения со скоростью 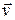к подвижной стороне необходимо будет прикладывать силу. Эта сила и совершает ту работу, которая выделяется в проводах контура при протекании по нему индукционного тока.

Сила 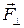совершает отрицательную работу, равную положительной работе составляющей силы Лоренца . Действительно, за время полная работа силы Лоренца

. (20.8)

Часто бывает так, что контур образован не одним витком, а несколькими. По сути дела именно такая ситуация реализуется, например, во всех трансформаторах. Витки соединяются последовательно, и ЭДС в таком контуре равна сумме ЭДС в каждом из витков:

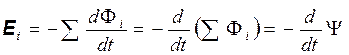. (20.8)

Величина

(20.9)

называется потокосцеплением.

Токи Фуко

Индукционные токи могут возникать не только в контурах, но и в сплошных массивных проводниках. Действительно, всякий сплошной проводник можно представить состоящим из большого количества замкнутых контуров. В этом случае индукционные токи называют вихревыми или токами Фуко.

По правилу Ленца вихревые токи направлены так, чтобы противодействовать причине их вызывающей. Поэтому движущиеся в магнитном поле сплошные проводники испытывают сильное торможение, величина которого зависит от скорости движения. Это используют, например, для торможения подвижных частей стрелочных приборов. При этом торможение уменьшается по мере приближения стрелки к положению равновесия.

В индукционных печах вихревые токи обеспечивают разогрев металлов до плавления.

Однако в трансформаторах индукционные токи приводят к дополнительным потерям энергии на разогрев сердечника, и с ними борются, набирая сердичники из изолированных пластин.

При протекании по проводам тока создается магнитное поле, и носители заряда движутся в этом поле. Если ток переменный, то возникающие токи Токи Фуко увеличивают его вблизи поверхности провода и уменьшают в центре. В результате большая часть переменного тока протекает по поверхности проводника. Это явление называют поверхностным, или скин-эффектом.