Определение расчетных усилий в балках методом линий влияния
Метод линий влияния принят при расчете балок, ферм, рамных конструкций и особенно при расчете мостовых, крановых и других инженерных сооружений с подвижной нагрузкой.
Линия влияния выражает зависимость усилия (или деформации) в каком-либо заданном сечении балки или элементе фермы от положения груза на них. В практических расчетах их всегда строят от одного груза, равного единице, и после этого построения используют для определения усилий (или деформаций) в изучаемом сечении или элементе при любом заданном загружении от нескольких сосредоточенных сил или распределенных нагрузок.
Линии влияния опорной реакции в однопролетной балке с шарнирными опорами.
Линия влияния опорной реакции балки выражает зависимость величины реакции от положения груза, равного единице, на балке.
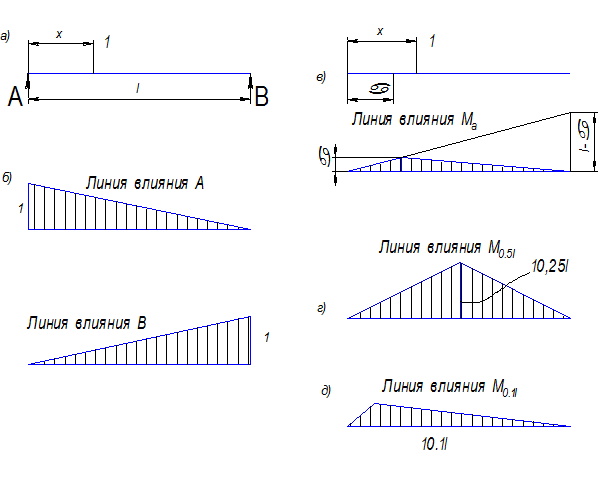 Рис. 8.1 К построению линии влияния опорных реакций и моментов в разных сечениях балки цифрами на рис д—з указаны наибольшие моменты в сечениях 0,5L, 0,4L и т д.
Рис. 8.1 К построению линии влияния опорных реакций и моментов в разных сечениях балки цифрами на рис д—з указаны наибольшие моменты в сечениях 0,5L, 0,4L и т д.
|
Обозначим расстояние груза до левой опоры через х, пролет балки—через L (Рис. 8.1, а).
Реакция 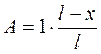
Реакция А определяется уравнением наклонной прямой (Рис. 8.1, б):
при х = 0 : А = 1:
при х = L : А = 0;
Подобным же образом строится линия влияния реакции В (Рис. 8.1, б).
Линии влияния изгибающего момента М.
Линия влияния изгибающего момента М выражает зависимость величины момента в заданном сечении от положения груза, равного единице, на балке.
Допустим, что груз находится справа на расстоянии x от опоры (Рис. 8.1, б).
При этом изгибающий момент равен:
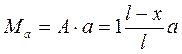
Построим линию влияния момента М (Рис. 8.1, а) из условия, что
при х = 0 : Мa = 1·а;
при х = L : Мa = 0.
Так как было сделано предположение, что груз находится справа от сечения а, то построенная прямая верна лишь на участке x≥а.
Допустим, что груз находится слева на расстоянии а от опоры.
Изгибающий момент целесообразно выразить в этом случае через величину правой опорной реакции 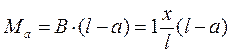
где В—опорная реакция на правой опоре.
При х = 0 : Ма = 0;
при х = L : Мa = L-a.
Так как было предположено, что груз находится слева от сечения а, то построенная прямая верна лишь на участке х≤а.
Подобным образом линии влияния М строятся для разных сечений балки. Ординаты линий влияния М имеют размерность длины.
Линия влияния поперечной силы Q выражает зависимость
величины поперечной силы в заданном сечении а от положения груза, равного единице, на балке.
Допустим, что груз находится справа от сечения а (Рис. 8.2 , а)
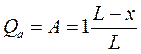
Прямая верна на участке x≥а.
Допустим, что груз находится слева от сечения а. При этом
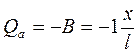
при х = 0 : 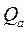 = 0;
= 0;
при х = I : 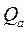 = - 1.
= - 1.
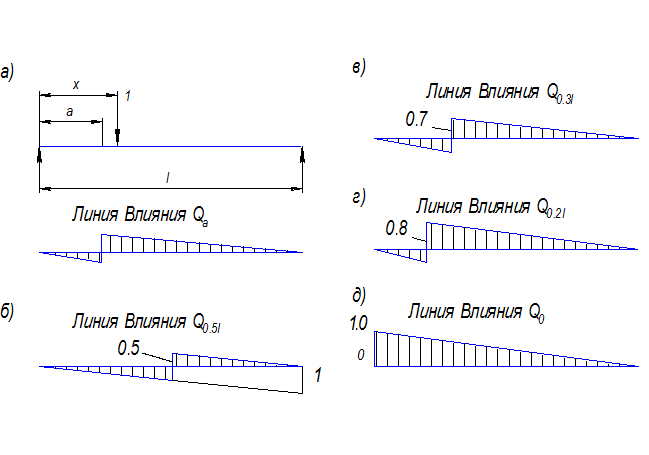 Рис. 8.2 К построению линий влияния поперечной силы в балках.
Рис. 8.2 К построению линий влияния поперечной силы в балках.
|
Эта линия верна на участке х≤а, под исследуемым сечением она меняет знак.
Ординаты линий влияния 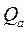 безразмерны.
безразмерны.
Использование линий влияния для определения усилий от системы сосредоточенных сил Р и равномерно распределенной нагрузки q.
Построенной линией влияния пользуются для определения усилия в заданном сечении балки от различной комбинации сосредоточенных и сплошных нагрузок.
Предположим, что для сечения на расстоянии а балки построена линия влияния некоторого усилия R, имеющая вид, показанный на Рис. 8.3,а.
Балка нагружена сосредоточенными силами 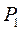 ,
, 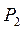 ,
, 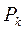 и равномерной нагрузкой q; на участке L—а.
и равномерной нагрузкой q; на участке L—а.
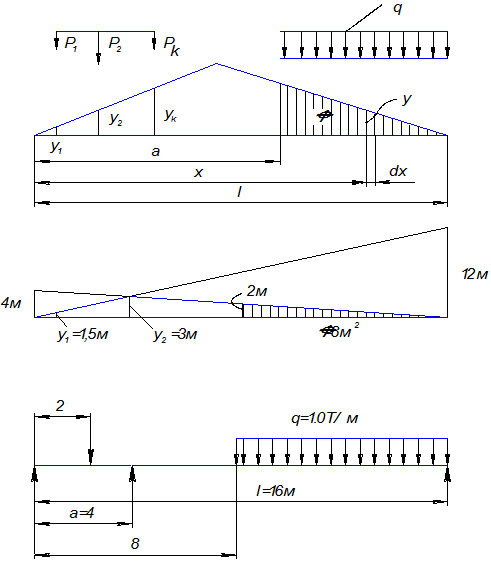 Рис. 8.3 Определение усилий от Р и q на основе построенных линий влияния:
а) общее положение; б), в) к численному примеру расчета
Рис. 8.3 Определение усилий от Р и q на основе построенных линий влияния:
а) общее положение; б), в) к численному примеру расчета
|
Ординаты линии влияния под силами  ,
,  ,
, 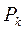 обозначим соответственно
обозначим соответственно 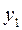 ,
, 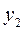 ,
, 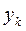 .
.
Пользуясь принципом независимости действия сил, находим усилие в сечении
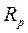 = = 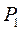 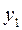 + + 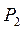 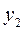 + + 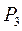 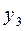 =Σ =Σ 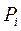 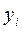 
| ( 8.1) |
Усилие от равномерной нагрузки найдем, заменив сосредоточенную нагрузку бесконечно большим количеством бесконечно малых сосредоточенных сил
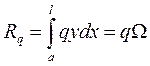
| (8.11) |
где Ω — площадь линии влияния на длине загруженного участка.
Полное усилие:
| R=ΣPiyi+qΩ | (8.12) |
R выражает собой продольную силу N, поперечную силу Q, момент М и т. д., в зависимости от построения линий влияния.
Дата добавления: 2016-05-25; просмотров: 1862;
