ОПРЕДЕЛЕНИЕ КРИВИЗНЫ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ НА ОСНОВЕ НЕЛИНЕЙНОЙ ДЕФОРМАЦИОННОЙ МОДЕЛИ
4.27. Значение кривизны принимают равным:
при двухзначной эпюре деформации по сечению - 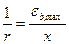 ;
;
при однозначной эпюре деформаций сжатого бетона по сечению - 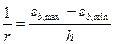
где εb,max и εb,min -максимальные и минимальные деформации бетона, определяемые на основе положений, приведенных в п.п.3.72-3.75;
х - высота сжатой зоны в направлении, нормальном к нейтральной оси;
h - высота сечения в направлении, нормальном условной нейтральной оси (черт 3.39,6);
при однозначной эпюре деформаций растянутой арматуры по сечению - 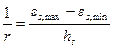
где εs,max и εs,min - абсолютные значения деформаций максимально и минимально растянутых стержней арматуры, определяемые согласно п.п.3.72-3.75;
hs - расстояние между этими стержнями в направлении, нормальном условной нейтральной оси.
При этом для элемента с трещинами в растянутой зоне напряжения в арматуре, пересекающей трещину, определяется по формуле
σsi = Es (εsi +0,8εs,crc), (4.50)
где εsi -усредненная относительная деформация растянутой арматуры в рассматриваемой стадии расчета, соответствующая линейному закону распределения деформаций по сечению;
εs,crc - относительная деформация растянутой арматуры в сечении с трещиной сразу после образования трещин (т.е. при действии момента Мсrс), равная εs,crc = σs,crc / Es, где σs,crc - см. п.4.13.
При наличии трещин напряженно-деформированное состояние сжатого бетона определяется по двухлинейной диаграмме σb – εb с использованием приведенного модуля деформаций сжатого бетона Eb.red, определяемого согласно п.4.24, и значений εb0 и εb2, принимаемых по табл.4.7.
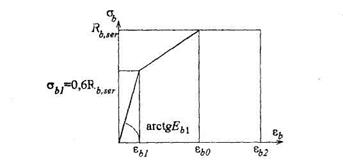
При отсутствии трещин напряженно-деформированное состояние сжатого бетона определяется по трехлинейной диаграмме (черт.4.8), где 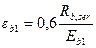 , εb0 и εb2 -см. табл.4.7; Eb1принимается равным: при непродолжительном действии нагрузки - Eb, при продолжительном действии нагрузки - см. формулу (4.41). Напряженно-деформированное состояние растянутого бетона также определяется по трехлинейной диаграмме (см. черт.4.8) с заменой Rb,ser на Rbt,ser, εb0 на εbt0, εb2 на εbt2, где значения εbt0 и εbt2 - см. табл.4.7
, εb0 и εb2 -см. табл.4.7; Eb1принимается равным: при непродолжительном действии нагрузки - Eb, при продолжительном действии нагрузки - см. формулу (4.41). Напряженно-деформированное состояние растянутого бетона также определяется по трехлинейной диаграмме (см. черт.4.8) с заменой Rb,ser на Rbt,ser, εb0 на εbt0, εb2 на εbt2, где значения εbt0 и εbt2 - см. табл.4.7
Таблица 4.7
| Характер действия нагрузки | Относительные деформации бетона | |||||
| при сжатии | при растяжении | |||||
| εb0·103 | εb2·103 | εb1,red·103 | εbt0·103 | εbt2·103 | εbt1,red·103 | |
| непродолжительное | 2,0 | 3,5 | 1,5 | 0,10 | 0,15 | 0,08 |
| продолжительное при относительной влажности окружающего воздуха, % | ||||||
| выше 75 | 3,0 | 4,2 | 2,4 | 0,21 | 0,27 | 0,19 |
| 40-75 | 3,4 | 4,8 | 2,8 | 0,24 | 0,31 | 0,22 |
| ниже 40 | 4,0 | 5,6 | 3,4 | 0,28 | 0,36 | 0,26 |
Дата добавления: 2016-05-25; просмотров: 695;
