Черт.3.43. К примеру расчета 38
Требуется проверить прочность элемента на действие крутящих и изгибающих моментов, а также на совместное действие крутящих моментов и поперечных сил.
Расчет. Рассматриваем сечение как прямоугольное, не учитывая "в запас" полку ригеля. Размеры этого сечения принимаем равными b =300 мм, h = 800 мм.
Расчеты производим согласно пп.3.77-3.80.
Проверяем условие (3.152) на действие максимального крутящего момента Т = 84 кНм.
0,1Rbb2h = 0,1·14,5·3002·800 = 104,4·106Н·мм = 104,4 кН·м > T = 84 кНм,
т.е. условие выполняется.
Проверим прочность пространственного сечения со сжатой стороной по нижней грани, расположенной у опорного сечения, на совместное действие крутящих и изгибающих моментов из условия (3.153).
Определяем согласно п.3.19 предельный изгибающий момент.
Из черт.3.43,а находим: As1 = 2413 мм2(3Æ32), А's1= 1388 мм2 (2Æ20+2Æ22), а' = 68 мм; ho = 800 - 60 = 740 мм. Из формулы (3.16) имеем
.
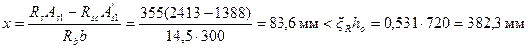Тогда
M0 = Rbbx(ho - 0,5х) + RsА's(ho - a') =
=14,5·300·83,6· (740-0,5·83,6) + 355·1388· (740-68) = 585·106 Н·мм.
Определим предельный крутящий момент Тo.
Горизонтальные поперечные стержни согласно черт.3.43,а Æ14 и шагом sw= 100 мм. Тогда
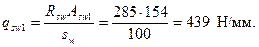
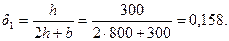
Поскольку RsАs1= 355·2413 = 856620 H > 2qsw1b = 2·439·300 = 263400 H, значение То определяем по формуле (3.160)
а моменты M и Т определяем при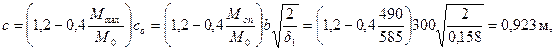 
т.е.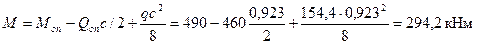 
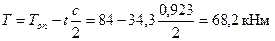
Проверяем условие (3.153):
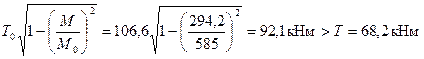
т.е. прочность на совместное действие изгибающих и крутящих моментов у опоры обеспечена.
Проверяем прочность пространственного сечения со сжатой стороной по боковой грани, на совместное действие крутящих моментов и поперечных сил, располагая это сечение у опоры. Предварительно проверим условие (3.162), принимая, согласно вычисленному выше, T01= 104,4 кН. м и вычислив из условия (3.43) Q01= 0,3Rbbho = 0,3·14,5·300·740 = 965700 Н = 965,7 кН.
Значения Т и Q определяем в сечении на расстоянии, а = 2b + h = 2·300 + 800 = 1400 мм = 1,4 м от опоры, т. е
Т = Ton - ta = 84 - 34,3·1,4 = 36 кНм;
Q = Qon - qa = 460-154,4·1,4 = 243,8 кНм.
Тогда
т. е условие (3.162) выполнено.
Из черт.3.43,а находим As2 = 804 + 314 + 380 = 1498 мм2 (Æ32 + Æ20 + Æ22).
Шаг и диаметр вертикальных хомутов тот же, что для горизонтальных стержней, поэтому qsw2 = qsw1 = 439 Н/мм.
Поскольку RsAs2= 355·1498 = 531790 Н < 2qsw2h = 2·439·800 = 702400 Н, значение. То равно
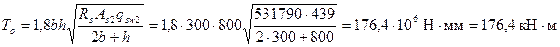
Определяем согласно п.3.31 значение Q и значение Qo как правую часть условия (3.44).
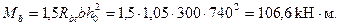
При двухветвевых хомутах qsw = 2qsw2= 2·439 = 878 Н/мм.
Определим невыгоднейшее значение с согласно п.3.32, принимая q1 = 100 кН/м. Поскольку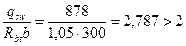 
, значение с равно 
.
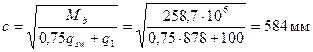Принимая сo = с = 584 мм < 2ho, имеем
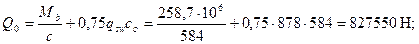
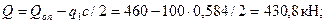
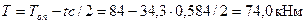
Проверяем условие (3.163)
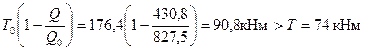
т.е. прочность при совместном действии изгибающих моментов и поперечных сил обеспечена.
Как видно из черт.3.43,б и д,в нормальном сечении с наибольшим пролетным изгибающим моментом имеет место крутящий момент, поэтому следует проверить пространственное сечение, середина проекции которого располагается в этом нормальном сечении, на действие моментов М = 321 кНм и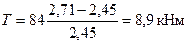 
При этом растянутая сторона пространственного сечения располагается по нижней грани.
Определим предельный изгибающий момент Мо. Для этой части ригеля средний верхний стержень Æ32 оборван, и поэтому согласно черт.3.43,а имеем А's1= 1609 мм2(2Æ32); а' = 60 мм; Аs1 = 1388 мм2 (2Æ20+2Æ22); а = 68 мм; hо = 800 - 68 =732 мм.
Высота сжатой зоны равна
следовательно, значение Мо определяем по формуле (3.19):
Мо = RsAs1(ho - a')= 355·1388· (732-60) = 331,1·106 Нмм = 331,1 кНм
Горизонтальные поперечные стержни Æ14 в этой части ригеля имеют шаг sw = 200 мм; отсюда
Поскольку RsAs1 = 355·1388 = 492740 H > 2qsw1b =2·219,5·300 = 131700 Н,
значение То определяем по формуле (3.160):
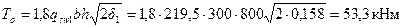
Проверяем условие (3.153)
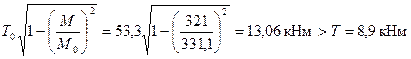
т.е. прочность этого сечения обеспечена.
Дата добавления: 2016-05-25; просмотров: 464;