Страховая статистика
В практике актуарных расчетов широко используется страховая статистика. Она представляет собой изучение и обобщение наиболее массовых и типичных страховых операций на основе статистических методов обработки натуральных и стоимостных показателей, характеризующих страховое дело. Показатели страховой статистики делятся на две группы. Первая группа отражает процесс формирования страхового фонда, вторая группа – его использование.
В обобщенном виде страховую статистику можно свести к анализу следующих показателей:
- число объектов страхования – n;
- число страховых событий – е;
- число пострадавших объектов в результате страховых событий – m;
- сумма собранных страховых платежей – ∑Р;
- сумма выплаченного страхового возмещения – ∑SВ;
- страховая сумма для всех объектов страхования – ∑Sn;
- страховая сумма, приходящаяся на поврежденный объект – ∑Sm.
Расчетные показатели страховой статистики:
1. Частота страховых событий – равна соотношению между числом страховых событий и числом застрахованных объектов, т.е. она показывает сколько страховых случаев приходится на один объект страхования
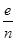< 1 (8.1)
Причем страховое событие может быть одно (град, землятресение), но вызвать многочисленные страховые случаи (пострадавшие объекты).
2. Опустошительность страхового события (коэффициент кумуляции риска) – отношение числа пострадавших объектов к числу страховых событий:
Ккум = m / e. (8.2)
Он показывает, сколько застрахованных достигает то или иное событие, иначе говоря, сколько страховых случаев происходит в результате одного события. Минимальный коэффициент кумуляции риска = 1. Если опустошительность > 1, то больше и кумуляция риска. Поэтому на практике страховые компании при страховании имущества стремятся избежать сделок, где есть большой коэффициент кумуляции.
3. Коэффициент убыточности (степень ущербности) – соотношение между суммой выплаченного страхового возмещения и страховой суммой всех пострадавших объектов, т.е.
Куб =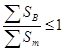 
(8.3)
4. Средняя страховая сумма на один объект страхования – отношение общей страховой суммы всех объектов страхования к числу застрахованных объектов, т.е.
Sn =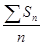 
. (8.4)
5. Средняя страховая сумма на один пострадавший объект – отношение страховой суммы всех пострадавших объектов на число этих объектов :
Sm =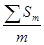 
. (8.5)
6.Тяжесть риска – отношение средних страховых сумм:
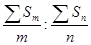. (8.6)
С помощью этого отношения производится оценка и переоценка частоты проявления страхового события.
7. Убыточность страховой суммы (вероятность ущерба) равна сумме выплаченного страхового возмещения, деленной на страховую сумму всех объектов страхования:
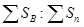. (8.7)
Показателем величины риска является число < 1. Обратное соотношение недопустимо, так как это означает недострахование.
- Норма убыточности – это соотношение суммы выплаченного страхового возмещения, выраженное в процентах к сумме собранных страховых платежей
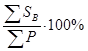. (8.8)
Для практических целей исчисляют нетто-норму и брутто-норму убыточности. Этот показатель может быть < 1, = 1, >1. Величина нормы убыточности свидетельствует о финансовой стабильности данного вида страхования.
9. Частота ущерба. Определяется как произведение частоты страховых случаев и опустошительности
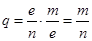< 1 (8.9)
Данный показатель отражает частоту наступления страхового случая. Всегда < 1. Если q = 1, это означает достоверность наступления страхового события для всех объектов. Выражается в % (или промилле) к числу объектов страхования.
Кроме того, должны быть установлены факторы, влияющие на частоту ущерба. Это позволяет выявить группы риска.
10. Тяжесть ущерба. В некоторых видах страхования возможны страховые случаи, которые причиняют ущерб, равный действительной стоимости застрахованного имущества. Такой ущерб называется полным. Однако в большинстве видов имущественного страхования ущерб меньше действительной стоимости имущества, которое не уничтожено, а только повреждено. Такой ущерб называется частичным.
Тяжесть ущерба можно выразить математически как произведение коэффициента ущербности (∑SB : ∑Sm) и соотношения средних страховых сумм:
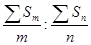, (8.10)
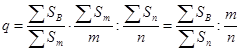, (8.11)
где n – число застрахованных объектов;
∑Sn – страховая сумма по всем договорам;
m – число пострадавших объектов;
∑Sm – страховая сумма по всем пострадавшим объектам.
Следовательно:
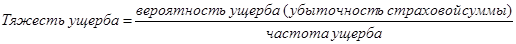(8.12)
Тяжесть ущерба (степень, объем ущерба, вероятность распространения ущерба) показывает, какая часть страховой суммы уничтожена. Снижается с увеличением страховой суммы.
Теоретической основой определения степени вероятности дефицита средств является так называемый «коэффициент профессора Ф.В. Коньшина»
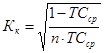, (8.13)
где n – число застрахованных объектов;
ТСср – средняя тарифная ставка по всему страховому портфелю.
Чем меньше будет значение К, тем ниже вероятность дефицитности средств и тем выше финансовая устойчивость страховой компании.
Однако данный коэффициент дает наиболее точные результаты в тех случаях, когда страховой портфель страховщика состоит из объектов с примерно одинаковыми страховыми суммами (однородными по стоимости страховыми рисками). На величину показателя К, как видно из формулы, не влияет величина страховой суммы (страхового покрытия), ее нет в формуле, а влияют лишь количество застрахованных объектов (n) и размеры средней тарифной ставки (ТСср). Иными словами, чем больше застрахованных объектов и выше размер страхового тарифа, тем меньше будет К и выше финансовая устойчивость страховых операций.
Для оценки финансовой устойчивости страхового фонда как отношения доходов к расходам за тарифный период (практический аспект), используется формула:
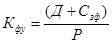, (8.14)
где Кфу – коэффициент финансовой устойчивости;
Д – сумма доходов страховщика за тарифный период;
Р – сумма расходов за тот же период;
Сзф – сумма средств в запасных фондах.
Нормальным состоянием финансовой устойчивости страховой организации, если Кфу > 1, т.е. когда сумма доходов с учетом остатка средств в запасных фондах превышает все расходы страховщика.
Дата добавления: 2016-05-25; просмотров: 937;