Конвективный теплообмен при движении среды в каналах
При движении жидкости (газа) в трубах или каналах максимальный размер пограничного слоя лимитируется радиусом трубы (канала). Поэтому по длине канала выделяется гидродинамический начальный участок или участок стабилизации, в пределах которого пограничные слои формируются независимо друг от друга, и область полностью развитого течения, где динамические слои от противоположных стенок сомкнулись на оси трубы и более не изменяются. В области развитого или, как говорят, стабилизированного течения устанавливается неизменный профиль скорости, уравнение которого определяется геометрией канала и режимом течения. Процесс стабилизации профиля скоростей происходит следующим образом. Вблизи входного сечения на поверхности трубы образуется динамический пограничный слой, толщина которого постепенно увеличивается по мере увеличения расстояния от входа в трубу. На некотором расстоянии от входа в трубу происходит смыкание слоев, и течение приобретает стабилизированный характер. На рисунке показано такое развитие процесса.
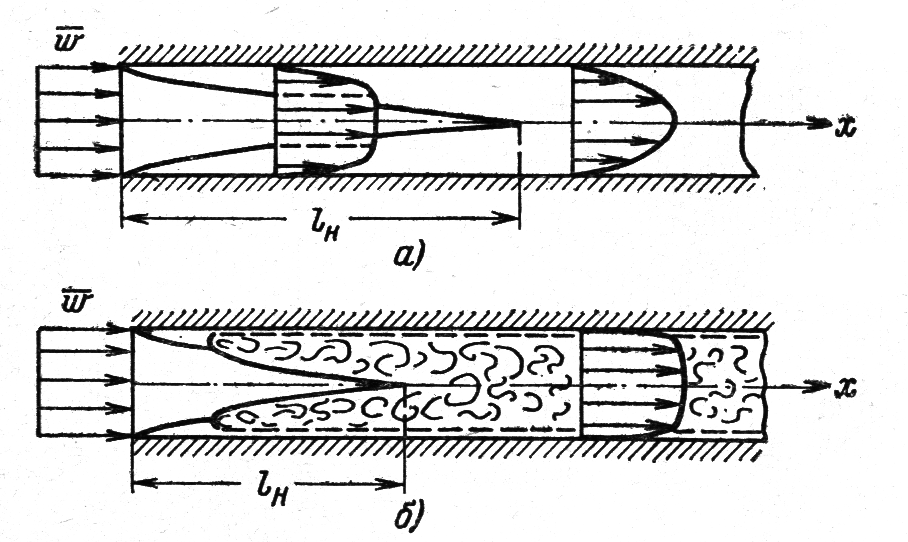
Если число подобия Рейнольдса для потока в трубе меньше критического
Reкр=wd/n < 5×105, то на всем протяжении начального участка течение в пограничном слое имеет ламинарный характер (см. рис. а)). Когда Re>Reкр, вблизи входного сечения сначала формируется ламинарный пограничный слой, который затем переходит в турбулентный, и после смыкания турбулентных пограничных слоев устанавливается стабилизированное турбулентное течение жидкости (см. рис. б)). При этом у самой поверхности в очень тонком вязком подслое сохраняется ламинарное течение жидкости.
Длина гидродинамического начального участка стабилизации потока при ламинарном режиме определяется соотношением
lн=0,05d Re,
то есть значение lн тем больше, чем выше число Re.
При турбулентном течении величина lн слабо зависит от Re и составляет примерно
lн @15d.
При ламинарном течении перенос теплоты в направлении нормали к стенке осуществляется теплопроводностью. В то же время каждый слой имеет различную скорость продольного движения. Поэтому наряду с поперечным переносом теплоты путем теплопроводности происходит также конвективный перенос теплоты в продольном направлении.
Рассмотрим развитие процесса теплообмена вдоль трубы. Пусть во входном сечении температура жидкости постоянна и по величине отличается от температуры стенки. По мере движения потока между жидкостью и стенкой происходит обмен теплотой и температура жидкости постепенно изменяется. Вначале вблизи от входного сечения изменение температуры происходит лишь в тонком слое около поверхности. Затем по мере удаления от входного сечения все большая часть потока вовлекается в процесс теплообмена. Около поверхности трубы образуется тепловой пограничный слой, толщина которого постепенно увеличивается в направлении движения потока. На некотором расстоянии от входа в трубу lн.т тепловые пограничные слои смыкаются, и в процессе теплообмена далее участвует весь поток жидкости. Расстояние lн.т может быть приближенно оценено по зависимости
lн.т =0,05 d Re Pr.
На расстоянии большем, чем lн.т профиль распределения температур по сечению трубы продолжает изменяться, как это показано на рисунке
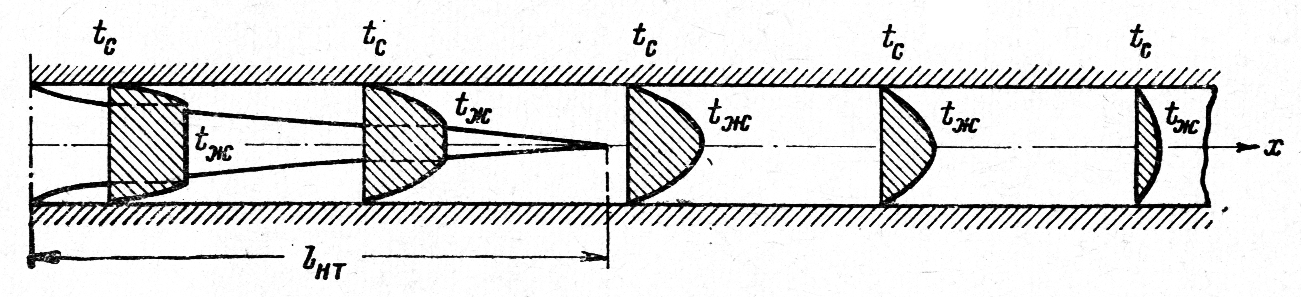
В пределах теплового начального участка стабилизации температурный градиент в жидкости у стенки убывает по мере увеличения расстояния от входа быстрее, чем температурный напор, так как центральная часть потока еще не участвует в теплообмене. Поэтому из уравнения теплоотдачи

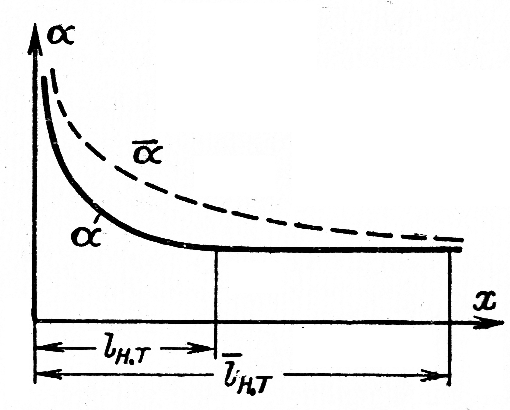 Следует, что локальный коэффициент теплоотдачи aлок постепенно уменьшается вдоль трубы. Падение локального коэффициента теплоотдачи продолжается до тех пор, пока тепловые пограничные слои не смыкаются. Далее градиент температуры и температурный напор убывают с одинаковой скоростью, а локальный коэффициент теплоотдачи принимает постоянное значение. На рисунке показано изменение локального и среднего коэффициентов теплоотдачи в зависимости от длины трубы. Этот график показывает, что расстояние, на котором происходит стабилизация средних коэффициентов теплоотдачи, всегда больше расстояния, отвечающего стабилизации локальных коэффициентов теплоотдачи. Опытами и расчетами показано, что при отношении длины трубы к ее диаметру более 50 изменением коэффициента теплоотдачи на начальном участке можно пренебречь. В остальных рекомендуется ввести поправочный коэффициент eL :
Следует, что локальный коэффициент теплоотдачи aлок постепенно уменьшается вдоль трубы. Падение локального коэффициента теплоотдачи продолжается до тех пор, пока тепловые пограничные слои не смыкаются. Далее градиент температуры и температурный напор убывают с одинаковой скоростью, а локальный коэффициент теплоотдачи принимает постоянное значение. На рисунке показано изменение локального и среднего коэффициентов теплоотдачи в зависимости от длины трубы. Этот график показывает, что расстояние, на котором происходит стабилизация средних коэффициентов теплоотдачи, всегда больше расстояния, отвечающего стабилизации локальных коэффициентов теплоотдачи. Опытами и расчетами показано, что при отношении длины трубы к ее диаметру более 50 изменением коэффициента теплоотдачи на начальном участке можно пренебречь. В остальных рекомендуется ввести поправочный коэффициент eL :
a=eL aр.
Значения eL приведены в таблице.
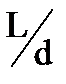
| |||||||||
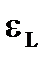
| 1.9 | 1.7 | 1.4 | 1.3 | 1.2 | 1.1 | 1.05 | 1.02 |
При расчетах теплоотдачи необходимо учитывать изменение температуры жидкости вдоль трубы вследствие теплообмена. Среднее значение температуры жидкости может быть определено арифметическим усреднением температур в начальном и конечном сечениях трубы или другим способом, обеспечивающим требуемую точность расчета.
Значительное влияние на интенсивность теплоотдачи может оказывать изменение теплофизических свойств жидкости (в первую очередь вязкости) от температуры. При охлаждении жидкости ее температура у стенки ниже, а вязкость выше, чем в ядре потока. Поэтому по сравнению с изотермическим потоком скорость у стенки ниже, а в ядре потока выше. При нагревании жидкости наоборот, скорость течения жидкости у стенки выше, а в ядре потока ниже. Изменение поля вязкости и скорости у стенки при изменении направления теплового потока приводит к изменению интенсивности теплоотдачи для капельных жидкостей. Это учитывается введением в уравнение теплоотдачи симплекса (Prж/Prст). Для газов симплекс (Prж/Prст)=1.
Ламинарный режим течения характеризуется вялым движением жидкости при котором в результате разности температур жидкости и стенки возможно образование конвективных токов в поперечном сечении потока (свободная конвекция). Поэтому в уравнении теплоотдачи присутствует число подобия Грасгофа:
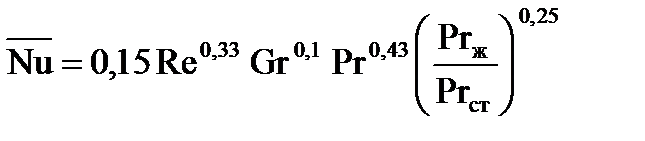 .
.
В качестве определяющей температуры при расчетах чисел подобия следует принимать температуру жидкости, а в качестве определяющего размера для круглых труб – внутренний диаметр; для других форм сечений - эквивалентный диаметр.
Теплоотдача при турбулентном режиме течения
При турбулентном режиме течения (Re>104) вследствие интенсивного перемешивания температура в ядре потока практически постоянная, а резкое ее изменение имеет место только в при стенном ламинарном слое. При таких условиях свободное движение в поперечном сечении канала практически не развивается, а интенсивность теплоотдачи полностью определяется величинами, которые характеризуют вынужденное движение потока.
На основании опытных данных для прямых труб рекомендуется следующая формула:
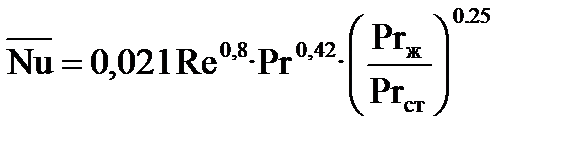
За определяющую температуру здесь принята средняя температура жидкости, а за определяющий размер – внутренний диаметр трубы или эквивалентный диаметр канала.
Согласно физическим представлениям этого процесса интенсивность теплоотдачи зависит от степени турбулентности потока, физических свойств жидкости и направления теплового потока.
| L/d Re | ||||||||
| 1×104 | 1.65 | 1.50 | 1.34 | 1.23 | 1.17 | 1.13 | 1.07 | 1.03 |
| 2×104 | 1.51 | 1.40 | 1.27 | 1.18 | 1.13 | 1.10 | 1.05 | 1.02 |
| 5×104 | 1.34 | 1.27 | 1.18 | 1.13 | 1.10 | 1.08 | 1.04 | 1.02 |
| 1×105 | 1.28 | 1.22 | 1.15 | 1.10 | 1.08 | 1.06 | 1.03 | 1.02 |
| 1×106 | 1.14 | 1.11 | 1.08 | 1.05 | 1.04 | 1.02 | 1.02 | 1.01 |
Надежность формулы проверена для значений Re < 5×106. Для относительно коротких труб (L/d<50), когда стабилизация теплообмена не наступила, необходимо ввести поправку eL, величина которой выбирают из таблицы:
Теплоотдача при переходном режиме движения жидкости
Переходной режим течения наблюдается при значениях числа подобия Рейнольдса 2×103 < Re < 104 . Вследствие сложности процесса, обусловленного одновременным проявлением особенностей ламинарного и турбулентного режимов в потоке, пока не удалось сделать надежных обобщений для расчетов теплоотдачи в этом режиме. Приближенно рассчитать коэффициенты теплоотдачи в этом режиме можно по формуле:
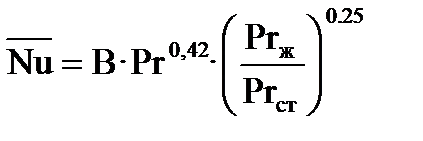 .
.
Значения величины В выбирают из таблицы
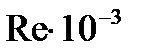
| 2.2 | 2.3 | 2.5 | 3.5 | |||||
| B | 2.2 | 3.6 | 4.4 | 7.5 | 12.2 | 16.5 |
Теплоотдача при течении жидкости в изогнутых трубах
При движении в изогнутых трубах в жидкости возникают центробежные силы, создающие в поперечном сечении циркуляционные токи. В результате возникает сложное движение жидкости по винтовой линии. Экспериментально установлено, что такая циркуляция возникает при 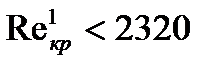 для прямой трубы.
для прямой трубы.
Для определения 
 при течении жидкости в винтовых змеевиках предложена формула:
при течении жидкости в винтовых змеевиках предложена формула:
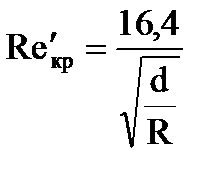 ,
,
где : d - диаметр трубки; R - радиус закругления змеевика.
Если 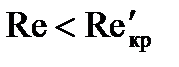 , то пользуемся формулой для ламинарного движения жидкости по прямой трубе.
, то пользуемся формулой для ламинарного движения жидкости по прямой трубе.
При 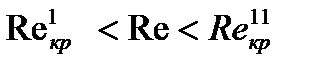 расчеты теплоотдачи следует вести по формуле для турбулентного режима течения в прямых трубах. В этой области имеет место ламинарный режим движения жидкости с циркуляцией потока внутри трубы.
расчеты теплоотдачи следует вести по формуле для турбулентного режима течения в прямых трубах. В этой области имеет место ламинарный режим движения жидкости с циркуляцией потока внутри трубы.
При 
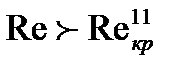 наблюдается турбулентное течение жидкости при наличии циркуляции. Граница перехода к такому течению может быть определена по выражению:
наблюдается турбулентное течение жидкости при наличии циркуляции. Граница перехода к такому течению может быть определена по выражению:
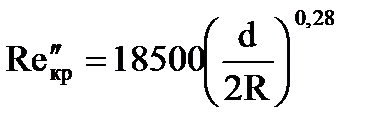
 .
.
Для этой области расчет ведут по формуле для турбулентного режима движения с коррекцией на циркуляцию e изг::
e изг = 1+1,8d/R.
Дата добавления: 2016-05-05; просмотров: 2629;
