Конструкции структур и узлы сопряжений
Конструктивные решения структурных плит отличаются столь большим многообразием, что нет возможности описать их все подробно. В мировой практике применения структур насчитывается около 130 различных систем, отличающихся прежде всего конструкцией узла сопряжения стержней. Именно в узле сопряжения сосредоточены главные особенности технологии изготовления и сборки конструкции, определяющие отличия одной системы от других.
Одной из первых нашла применение в строительстве система немецкой фирмы "Меро" (1942 г.), предложившей пространственно-стержневые сборно-разборные каркасы кристаллического строения для зданий военного назначения. Позднее такие конструкции нашли применение и в мирном строительстве. В отечественной практике эта система была несколько усовершенствована В.К. Файбишенко и другими конструкторами и получила название "системы МАрхИ" (Московский архитектурный институт).
Узел системы "Меро" (МАрхИ) состоит из литого сферического, полусферического, либо многогранного элемента-коннектора с высверленными в нем отверстиями для болтов по числу примыкающих стержней (рис. 7.7). Иногда коннекторы изготовляют из стержневых заготовок многогранного (например, шестигранного) сечения. Болт пропускают в отверстие плоского цилиндрического вкладыша, запрессованного в торец трубчатого стержня и приваренного к нему. Между торцами коннектора и вкладыша размещают поводковую втулку шестигранного сечения с отверстием под болт, снабженную штифтовым фиксатором. Болт с помощью втулки завинчивают в коннектор до плотного касания между втулкой и торцевыми поверхностями, что обеспечивает передачу сжимающих усилий через втулку и площадки касания, а растягивающих - через болт. Стержни этой системы обладают высокой компенсационной способностью, что облегчает сборку. Компенсационной способностью называют возможность сборки, не взирая на неточности изготовления стержней. Недостатком конструкции является относительно высокая трудоемкость изготовления элементов узла. Система сборно-разборная, трудоемкость монтажа 1...1,5 чел.·ч/м2 перекрываемой площади.
Структуры МАрхИ базируются на применении унифицированных стержней и узловых коннекторов. Стержни из круглых труб с диаметром и толщиной от 60/3 до 146/10 имеют длину 1,5; 2 и 3 м. Общее число типов сечений унифицированных стержней обычно не превышает 10. В одной плите, как правило, используют не более 4...5 типов сечений. При
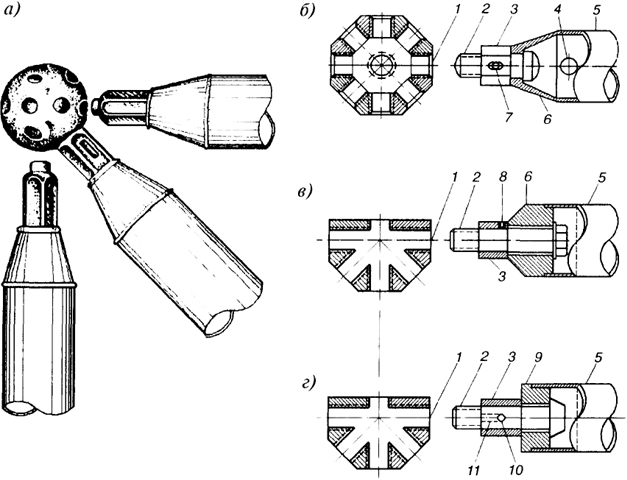
Рис. 7.7. Узловое соединение "Меро" и его модификации:
а, б - общий вид узла, узловой элемент и детали стержня системы "Меро"; в, г - детали трубчатых элементов в соединениях систем "Веймар" и "МАрхИ"; 1 - отверстие с внутренней резьбой; 2 - болт; 3 - поводковая гайка; 4 - монтажное отверстие; 5 - труба; 6 - оголовок трубы; 7 - ведущий палец; 8 - фиксатор; 9 - шайба; 10 - штифт; 11 - прорезь в гайке
длине стержней 3 м высота плиты составляет 2,12 м. Плиты предназначены для пролетов 18...36 м, при необходимости предусматривают консоли за счет смещения опорных конструкций от краев плиты к центру. Сечение коннекторов в плане - восьмиугольник, при этом используют два типа коннекторов с наибольшими размерами в плане 120×120 и 150×150 мм.
В системе "Октаплатт" (ФРГ, 1957 г.) сделана попытка облегчить и упростить узлы. Узловой элемент выполняют здесь в виде полого шара из двух штампованных половин, сваренных на подкладных кольцах. Стержни из труб, обрезанные под прямым углом, приваривают к шаровым элементам на монтаже (рис. 7.8, а). Достоинства узла заключаются не только в его относительной простоте, но и в свободе примыкания стержней под любым углом. Недостатки - отсутствие компенсационной способности стержней и большой объем монтажной сварки. По данным авторов конструкции узла наибольшее усилие на стержень (при использовании труб диаметром 65...115 мм) составляет 350 кН и определяется несущей способностью сварного шва в примыкании к шару.
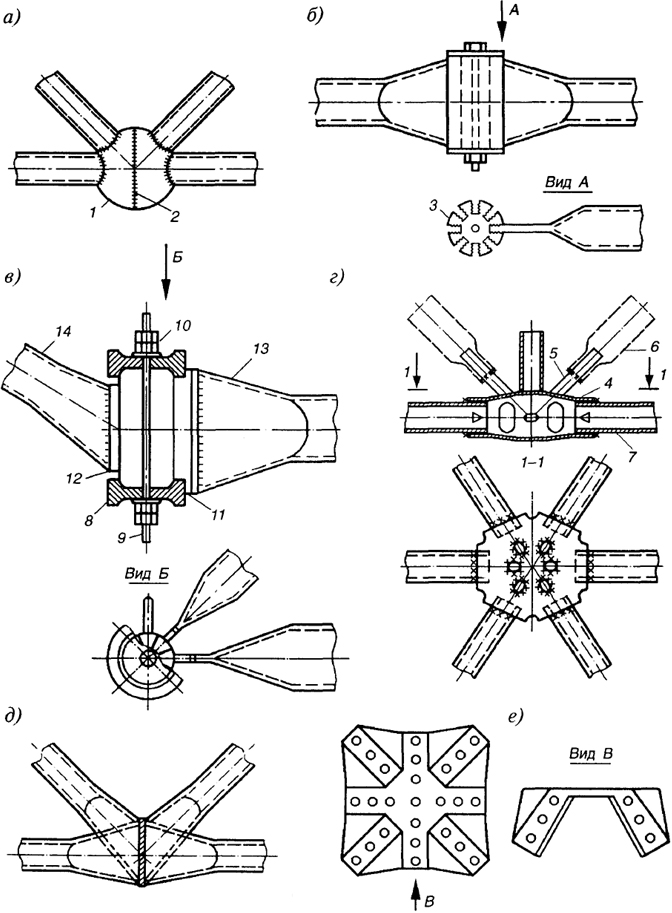
Рис. 7.8. Узлы различных структурных систем:
а - "Октаплатт"; б - "Триодетик"; в - "Берлин" ; г - "Дю Шато" ; д - узел ЦНИИСК; е - "Юнистрэт"; 1 - шаровая вставка; 2 - сварной шов; 3 - фигурная прорезь; 4 - крышка; 5 - круглый стержень; 6 - труба раскоса; 7 - труба нижнего пояса; 8 - крышка; 9 - стяжной стержень; 10 - гайка с контргайкой;11 - наконечник с приливом; 12 - то же, без прилива; 13 - стержень нижнего пояса (труба со сплющенным концом); 14 - труба раскоса
Система "Триодетик", разработанная в Канаде (1962 г., фирма "Фентимен"), привлекла внимание специалистов своей оригинальностью. Для соединения трубчатых стержней со сплющенными концами применяют узловой цилиндр с прорезями. Сплющенные концы труб подвергают специальной обработке в соответствии с прорезями (рис. 7.8, б). Все трубы, сходящиеся в узле, фиксируют в прорезях цилиндра одним зажимным болтом. Система была запроектирована для конструкций из алюминиевых сплавов, что позволяло использовать метод экструзии для получения стержневой заготовки специального профиля и изготовления узловых цилиндров простой нарезкой кусков из этой заготовки. Позднее появились структуры такой системы из стали с иной технологией производства узловых цилиндров (механическая обработка). Главное достоинство системы - малая трудоемкость сборки - 0,2 чел.·ч/м2.
Конструкция узла, близкая к только что рассмотренной, предложена для структур системы "Берлин". К сплющенным концам трубчатых стержней приваривают клиновидные калиброванные наконечники, образующие при сборе в узел цилиндр с отверстием внутри (рис. 7.8, в). Торцы цилиндра закрывают стальными крышками с бортами по наружному контуру и стягивают в узле шпильками. Растягивающие усилия в узле передаются наконечниками через крышки, а сжимающие - через плоскости контакта наконечников. Узел прост в сборке при условии высокой точности изготовления.
В узле системы "Дю Шато" (Франция) применены узловые штампованные фасонки (рис. 7.8, г). В каждой из двух фасовок предусмотрено по 6 полукруглых выемок, образующих после соединения фасонок узловой элемент с отверстиями для трубчатых стержней. Фасонки сваривают между собой по наружным линиям площадок касания. Стержни вставляют в отверстия и обваривают, образуя таким образом верхнюю или нижнюю сеть. Раскосы и стойки приваривают к наружным поверхностям узлового элемента (одной из фасонок). Узел обладает неплохой компенсационной способностью и довольно прост. Недостаток узла - большой объем монтажной сварки.
Система "Юнистрэт" (США) также основана на использовании штампованных фасонок (рис. 7.8, е), отличающихся тем, что при штамповке создается восемь плоскостей (по числу примыкающих стержней). В плоскостях выполняют отверстия для крепления стержней из прокатных или гнутых профилей (уголков, тавров, швеллеров и т.п.). Решение направлено на снижение трудозатрат при изготовлении и монтаже.
В узле "ЦНИИСК" (рис. 7.8, д) нет никаких дополнительных элементов. Концы труб сплющивают и в раскосах обрезают под нужным углом. Стержни при сборке закрепляют в специальном фиксаторе так, что между их торцами образуется свободное пространство, которое заполняют расплавленным
металлом в процессе ванной сварки. Предполагается, что узел образует равнопрочное соединение с основными стержнями. Основное достоинство узла - минимальная металлоемкость: расход расплавленного металла - около 1,5 % от массы структуры, тогда как в других решениях расход металла на образование узлов составляет 5...7 %, а в некоторых системах - более 10 %. Недостатки узла - ограниченная компенсационная способность и значительный объем монтажной сварки.
Для структур свойственно то же, что и для других конструктивных решений: их достоинства имеют и оборотную сторону. В целях унификации и удобства транспортирования трубы или прокатные профили длиной 12 м разрезают на короткие стержни, а затем из стержней (и узловых элементов) составляют поясные сетки. Всегда ли это необходимо? Конечно, не всегда. Возможны и иные решения, в которых кристаллические структуры создают с использованием плоских ферм, либо пространственных пирамид с основанием в виде треугольника, прямоугольника (квадрата), шестиугольника и т.п. Фермы (пирамиды) объединяют между собой в пространственную систему с помощью линейных элементов, длина которых также часто превышает размер ячейки поясной сетки (например, кратна ей).
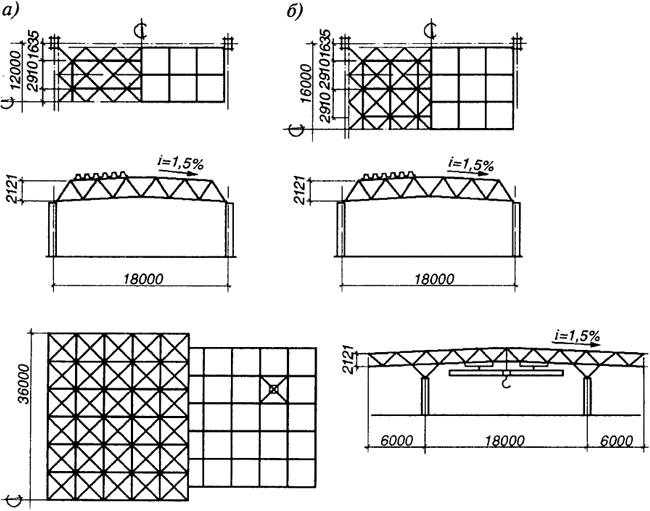
Рис. 7.9. Структурные плиты ЦНИИСК с элементами, изготовленными по унифицированному сортаменту
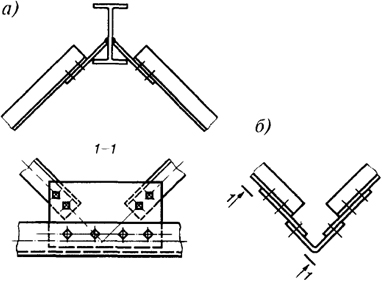
Рис. 7.10. Узлы структуры ЦНИИСК:
а - узел верхнего пояса; б - узел нижнего пояса
Наиболее широкое распространение в. покрытиях зданий получила в свое время конструкция структурных блоков "ЦНИИСК" с размерами в плане 12×18 и 12×24 м и высотой около 1,5 м, ориентированная на использование прокатных профилей (рис. 7.9, а, б). По конструктивной схеме - это складчатая система с поясами из двутавров и остальными элементами из одиночных равнополочных уголков. По верхним поясам, как по прогонам, на монтаже укладывают профилированный настил, служащий одновременно связевой системой. Элементы пространственной решетки крепят к поясам с помощью фасонок (рис. 7.10). Для повышения пространственной жесткости и надежности работы блоков "ЦНИИСК" в них предусмотрены наклонные торцевые фермы по короткой стороне. Для сокращения расхода металла и снижения трудозатрат при изготовлении и монтаже применялось разрежение решетки в средней части плиты. Блоки с разреженной решеткой получили название "Москва" (рис. 7.11, а, б).
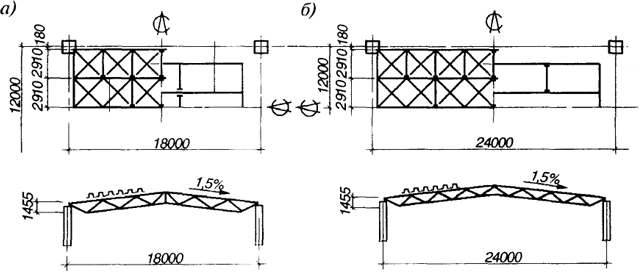
Рис. 7.11. Структурные блоки типа "Москва" с разреженной сеткой стержней
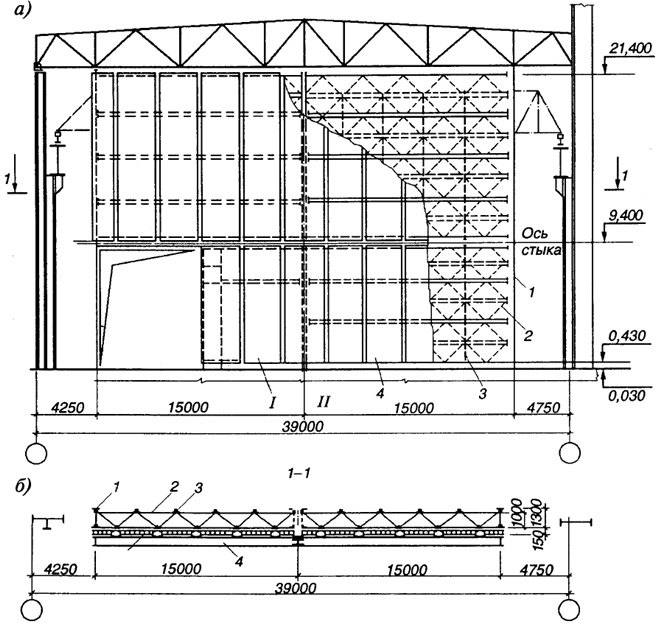
Рис. 7.12. Панельно-структурный торец машинного зала ТЭЦ:
a - фасад; б - горизонтальный разрез; 1 - продольная (вертикальная) ферма; 2 - поперечная ( наклонно расположенная) ферма; 3 - линейные элементы; 4 - облегченная панель ограждения
В энергетическом строительстве получили применение панельно-структурные временные торцевые стены главных корпусов ТЭЦ и ГРЭС (рис. 7.12). Включение легких стеновых панелей в работу структурной плиты и использование пространственной работы системы позволяет значительно облегчить стеновой каркас и обеспечить возможность сборки всей конструкции внизу для последующего подъема в проектное положение.1
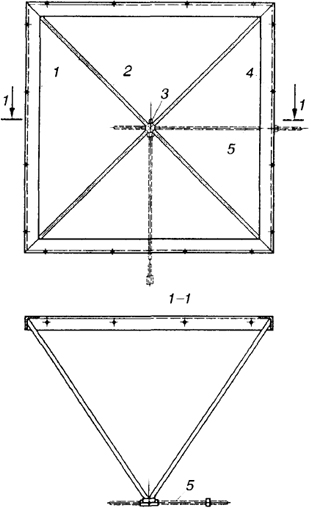
Рис. 7.13. Пирамида системы "Спэйс Дэк":
1 - рама из уголков; 2 - трубчатые раскосы; 3 - узловой элемент с отверстиями и внутренней резьбой; 4 - отверстия для монтажных болтов; 5 - стержни нижних поясов с правой и левой резьбой на концах
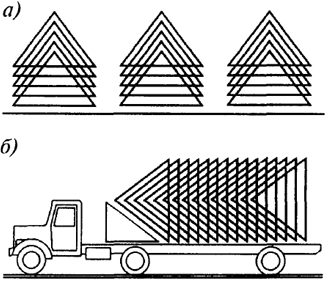
Рис. 7.14. Схемы компактной упаковки пирамид при складировании (а) и перевозке (б)
Примером системы, где основной конструктивной единицей является пирамида, можно назвать систему "Спэйс Дэк", разработанную еще в 50-е годы в Великобритании. Квадрат в основании пирамиды выполняют из одиночных уголков, ориентированных полками внутрь, а раскосы, образующие наклонные грани пирамиды, могут быть выполнены из труб, либо также из уголков (рис. 7.13). Основания пирамид, поставленных рядом, соединяют болтами, образуя ортогональную сетку одного из поясов, другую сетку образуют линейными элементами. Существует много других вариантов подобных конструкций, разработанных в отечественной практике, в том числе с пирамидами из тонколистовой стали. Достоинством таких конструкций является удобство компактной упаковки при транспортировании и складировании пирамид (рис. 7.14).
58 Купола. Конструирование и расчет
Купола применяют для покрытия круглых в плане зданий и сооружений диаметром до 100 м. Купольное покрытие состоит из двух основных конструктивных элементов: оболочки и опорного кольца. Для верхнего естественного освещения в куполе дополнительно устраивают верхнее фонарное кольцо. По расходу материалов купола более экономичны, чем другие пространственные покрытия. Чаще всего применяются сферические оболочки, образованные вращением вокруг вертикальной оси дуги круга. Оболочки куполов могут быть монолитными гладкими или сборными ребристыми. Монолитные купола имеют гладкую оболочку вращения, толщиной 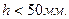 У мест примыкания к опорному кольцу оболочка утолщается.
У мест примыкания к опорному кольцу оболочка утолщается.
В настоящее время применяют в основном купола со сборными оболочками. Разрезка оболочки на элементы может быть меридиональной (для небольших куполов) или меридионально-кольцевой. В обоих случаях сборные элементы ребристые. Элементы большой длины криволинейные, малой длины – плоские. Опорное кольцо может быть сборным и монолитным.
В тонкостенном куполе при равномерно распределенной нагрузке на большей части оболочки развивается безмоментное напряженное состояние. Полное напряженное состояние – лишь вблизи опорного кольца. Кольцевыми изгибающими моментами М2 можно пренебречь. Поэтому тонкостенная оболочка с непрерывным по контуру шарнирно-подвижными опорами, совпадающими по направлению с касательной к оболочке, может быть рассчитана по безмоментной теории. Элемент оболочки, ограниченный двумя меридиональными и двумя кольцевыми сечениями находится под воздействием усилий 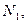
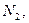 и
и 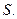
При осесимметричной нагрузке касательные усилия 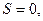 остаются лишь нормальные – меридиональные
остаются лишь нормальные – меридиональные 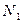 и кольцевые
и кольцевые 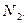
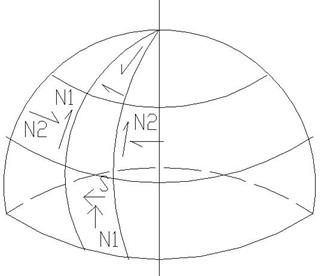
| 
|
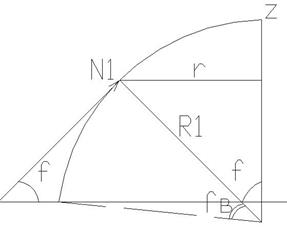
Из условия равновесия сегмента купола можно записать 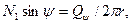 где
где 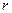 - радиус кольцевого сечения;
- радиус кольцевого сечения; 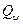 - нагрузка на сегмент купола, ограниченный углом
- нагрузка на сегмент купола, ограниченный углом 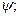
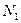 - меридиональное усилие, отнесенное к единице длины сечения. Меридиональное усилие
- меридиональное усилие, отнесенное к единице длины сечения. Меридиональное усилие 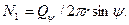
Горизонтальная проекция меридионального усилия 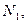 называемая распором
называемая распором 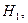 равна:
равна: 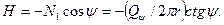 Уравнение равновесия купола
Уравнение равновесия купола 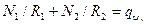 где
где 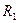 - радиус кривизны оболочки по меридиональному сечению;
- радиус кривизны оболочки по меридиональному сечению; 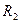 - то же по кольцевому;
- то же по кольцевому; 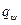 - составляющая нагрузки, нормальная к поверхности купола,
- составляющая нагрузки, нормальная к поверхности купола, 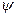 - текущая угловая координата.
- текущая угловая координата.
Зная усилие 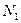 можно определить кольцевое усилие
можно определить кольцевое усилие 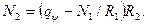
Из этих уравнений видно, что в меридиональном направлении оболочка вращения во всех точках испытывает сжатие. В колцевом направлении оболочка в верхней зоне сжата, в нижней – растянута, так как соотношение 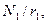 может быть как меньше, так и больше
может быть как меньше, так и больше 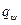
В реальных конструкциях оболочка купола имеет не безмоментное опирание, а упругое закрепление в опорном кольце. Поэтому по линии контакта оболочки и кольца возникают дополнительно статически неопределимые величины – меридиональный изгибающий момент 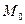 и радиальный распор
и радиальный распор 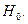 Их определяют из условия совместности деформаций оболочки и опорного кольца купола.
Их определяют из условия совместности деформаций оболочки и опорного кольца купола.
По мере удаления от опорного кольца изгибающий момент уменьшается, меняет знак и затухает.
От воздействия распора 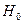 на опорное кольцо в нем возникает растягивающее усилие
на опорное кольцо в нем возникает растягивающее усилие 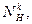 которое вызывает радиальное перемещение оси кольца. Распор
которое вызывает радиальное перемещение оси кольца. Распор 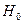 приложен к кольцу с эксцентриситетом
приложен к кольцу с эксцентриситетом 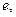 образуя момент
образуя момент 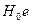 и кольцо поворачивается на угол
и кольцо поворачивается на угол 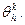 От воздействия момента
От воздействия момента 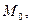 равномерно распределенного вдоль кольца в радиальном направлении возникает момент в кольцевом направлении
равномерно распределенного вдоль кольца в радиальном направлении возникает момент в кольцевом направлении 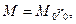 а его поперечные сечения поворачиваются на угол
а его поперечные сечения поворачиваются на угол 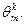 Опорное кольцо находится в условиях внецентренного растяжения. Вследвие малости изгибающего момента его можно рассчитывать как центрально-ратянутое.
Опорное кольцо находится в условиях внецентренного растяжения. Вследвие малости изгибающего момента его можно рассчитывать как центрально-ратянутое.
Оболочка монолитного купола, за исключением приопорных зон, сжата, армируется конструктивно одиночной сеткой из стержней диаметром 5-6 мм с шагом 150-200 мм. При толщине оболочки 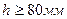 ставят двойную сетку. У опорного кольца ставят дополнительную меридиональную арматуру на восприятие опорного момента
ставят двойную сетку. У опорного кольца ставят дополнительную меридиональную арматуру на восприятие опорного момента 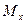 из стержней диаметром 6-8 мм и дополнительную кольцевую арматуру для восприятия
из стержней диаметром 6-8 мм и дополнительную кольцевую арматуру для восприятия 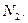 Рабочую арматуру опорного кольца ставят в виде кольцевых стержней диаметром 20-30мм, стыкуемых на сварке, чаще опорные кольца куполов подвергают предварительному обжатию посредством натяжения кольцевой рабочей арматуры.
Рабочую арматуру опорного кольца ставят в виде кольцевых стержней диаметром 20-30мм, стыкуемых на сварке, чаще опорные кольца куполов подвергают предварительному обжатию посредством натяжения кольцевой рабочей арматуры.
Напрягаемая арматура опорного кольца анкеруется на его выступах, расположенных по периметру в четырех, восьми и более местах в зависимости от диаметра кольца.
59 Гипары. Конструирование и расчет
Расчет гипаров
Гипары первой разновидности (см. рис, 11.4 а), Рассчитывают, используя уравнение поверхности (11 Л). В любом сечении, параллельном диагональному, представляющем собой параболу, параметр Кху— Z/(Xy) = Const. Для начала координат Кху =F/(Ab).
Из уравнения равновесия безмоментного напряженного состояния пологого гипара при равномерно распределенной нагрузке Q [6], [16];
2Kxy,Nxy = -Q (11.3)
Следует, что касательное усилие на единицу длины поверхности:
Nxy = - q/(2kxy) = - Qab/(2f). (11.4)
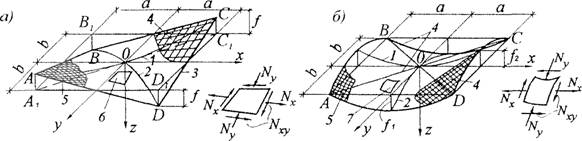
Рис. 11.4. Разновидности оболочек гипаров на прямоугольном (квадратном) плане и усилия безмоментного напряженного состояния в единичном элементе: А — линии главных кривизн поверхности направлены вдоль диагоналей основания; Б — линии главных кривизн параллельны сторонам основания; 1 — главная вогнутая парабола; 2 — То же, выпуклая; 3 — Прямолинейная образующая; 4 — Прямые линии поверхности; 5 — кривые линии поверхности; 6,7 — Единичные элементы оболочки
Нормальные усилия Nx = 0; Nv — 0 (кривизны в направлении прямолинейных образующих Кх = 0 И Kv — 0), т. е. безмоментное напряженное состояние гипара характеризуется только касательными усилиями постоянной интенсивности.
Главные усилия (вдоль линий главных парабол), определяемые по формуле (103) в Разделе 10, Численно равны касательным усилиям Nxy И постоянны по всей оболочке: одно из них — в направлении вогнутой параболы — растягивающее (Nm); Другое — в направлении выпуклой параболы — сжимающее (Nmc):
Nmt = - Nmc = ± Nxy = ± qab/(2f). (II.5)
В контурных (бортовых) элементах одиночных гипаров (рис. 1L5) Под действием сдвигающих усилий Nxy Возникает сжатие, достигающее наибольшей величины у опоры. Максимальное сжимающее усилие N& В бортовом элементе гипара с учетом утла ф его наклона к горизонтали определяется как сумма сдвигающих усилий Nxy По длине элемента:
Nb = 2Nxya /Costp. (11.6)
Вертикальная опорная реакция при опирании одиночного гипара на две опоры составляет:
Fy^2Qal (11.7)
Распор, направленный по опорной диагонали одиночного гипара,
Fh = 2Nxya^2.
(11.8)

 В)
В)
1-1
| Mi |
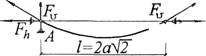
|
| ШГ Fh |
| ШШШПШШШШПШ Ч/2 |
| / |
| -^™»4. |
| %B ZSF\~ F'H L=2cNT I N^c |
 V ШШШШШПШШПШФ2
V ШШШШШПШШПШФ2
F
Рис. 11.5. К расчету одиночного гипара:
А — общий вид и схема усилий: Б — эпюра сжимающих усилий в бортовом элементе; В — план; / — плита; 2 — бортовой элемент; 3 — Опора; 4 — растянутая парабола; 5 — сжатая парабола
В составном покрытии, загруженном равномерно распределенной нагрузкой, каждая оболочкаможет быть рассчитана в первом приближении как одиночная.
Сдвигающие усилия от каждой оболочки передаются на коньковые ребра и элементы наружного контура, которые, в зависимости от типа покрытия, могут быть сжатыми или растянутыми (см. рис. 11,2), Например, в составном «четы-рехлепестковом» гипаре на квадратном плане (рис. 11.6 а) Горизонтальные коньковые ребра следует рассчитывать на суммарное усилие от двух оболочек:
Nh^0M -2NX}M, (11.9)
Где 0,85 — коэффициент, учитывающий краевой эффект при сочленении оболочек. В наклонных контурных элементах усилие вычисляется по формуле;
Nb = NXy®FcQs<P. (НЛО)
Усилие в наклонных коньковых ребрах покрытия (рис. 11.6 Б):
Nh = ft85 -2NX}m /cos<p, (11.11)
А в горизонтальных контурных элементах:
Nb = Nx>A. (11.12)
Вертикальная опорная реакция и усилие в затяжке при опирании составного гипара на четыре опоры (см. рис. 11.6 Б), соответственно, равны:
Fv = Qa* (11.13)
Fh^Nxya. (11.14)
Диафрагмы в виде ферм, арок, рам рассчитывают на касательные усилия, передающиеся соболочки, и вертикальные нагрузки, включая собственный вес диафрагмы.
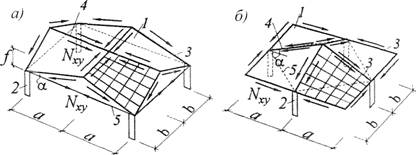
|
| Рис. 11.6. К расчету составных гипаров: А. б — варианты покрытий; 7 ■— оболочка; 2 — Опора; 3 — контурный (бортовой) элемент; 4 —-Коньковое ребро; 5 —- затяжка |
Напряженное состояние пологих гипаров на прямоугольном плане с криволинейными краями (см. рис. 11.4 б) Характеризуется нормальными сжимающими усилиями Nyj Направленными вдоль главной параболы положительной кривизны, растягивающими усилиями Л^ — вдоль главной параболы отрицательной кривизны и касательными усилиями Nxv Переменной интенсивности с макси-
Мальным значением на контуре оболочки. Их можно рассматривать как оболочки с поверхностью переноса и рассчитывать методом, разработанным для оболочек положительной кривизны [6], [16].
60 Цилиндрические оболочки. Резервуары и силосы. Особенности расчета
Дата добавления: 2016-05-25; просмотров: 9533;
