Течение и свойства жидкостей
1. Идеальная жидкость. Основные определения. Движение идеальной жидкости. Уравнение неразрывности. Уравнение Бернулли.
2. Движение вязкой жидкости. Уравнение Ньютона. Формула Пуазейля.
3. Модель кровообращения Франка. Электрическая модель кровообращения. Пульсовая волна. Формула Моенса-Кортевега.
1. Система кровообращения служит для постоянного снабжения клеток питательными веществами и газами, для обмена продуктами жизнедеятельности клеток, а также переноса тепла. Она представляет собой разветвленную и замкнутую цепь сосудов различного калибра. В этом она сходна с водопроводной системой, также предназначена для обмена водой и теплом между источником и многочисленными потребителями. В обеих системах движущей силой является давление, создаваемое на входе в систему и в участках выхода. Этой цели служит генератор давления, которым в системе кровообращения является сердце, а в водопроводной системе – насос.
Движение жидкости или крови всегда происходит от участка с более высоким давлением к участку со сниженным давлением, поэтому движение крови подчиняется тем же закономерностям, которые определяют движение жидкости в любой гидродинамической системе.
1.Воображаемая жидкость, совершенно не обладающая вязкостью называется идеальной. Уравнение неразрывности: произведение площади поперечного сечения трубки на скорость движения жидкости есть величина постоянная
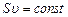 (1)
(1)
Пусть по наклонной трубке тока переменного сечения движется жидкость в направлении слева направо. Мысленно выделим область трубки, ограниченную сечениями 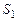 и
и 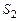 в которых скорости течения равны соответственно
в которых скорости течения равны соответственно 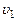 и
и 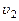 .
.
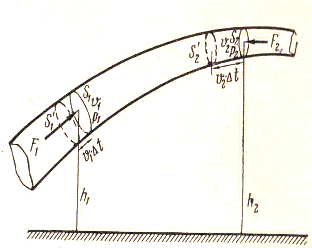
Определим изменение полной энергии в этой области за промежуток времени 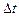 . За это время масса жидкости заключенная между сечениями
. За это время масса жидкости заключенная между сечениями 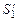 и
и 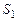 , втекает в рассматриваемую область, а масса, заключенная между
, втекает в рассматриваемую область, а масса, заключенная между 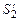 и
и 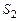 , вытекает из нее.
, вытекает из нее.
Полная энергия жидкости
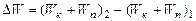 (2)
(2)
Или 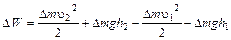 (3)
(3)
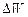 должна равняться работе
должна равняться работе 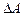 внешних сил по перемещению массы
внешних сил по перемещению массы 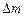
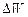 =
= 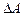 (4)
(4)
Определим 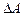 . Внешняя сила давления F1 совершает работу
. Внешняя сила давления F1 совершает работу 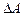 по перемещению втекающей массы на пути
по перемещению втекающей массы на пути 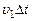 ; в то же время вытекающая масса совершает работу
; в то же время вытекающая масса совершает работу 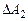 против внешней силы F2 на пути
против внешней силы F2 на пути 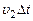 поэтому
поэтому
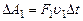 ,
, 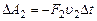 ,
, 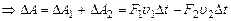
Учитывая, что 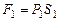 и
и 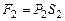 , где P1 и P2-давления на сечениях S1 и S2, получим
, где P1 и P2-давления на сечениях S1 и S2, получим 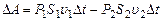 , но
, но 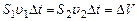
Где 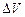 -объем каждой из рассматриваемых масс, поэтому
-объем каждой из рассматриваемых масс, поэтому 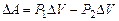 (5)
(5)
Объединяя формулы 3, 4, 5, получим: 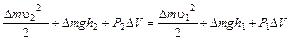
Поделив обе части на 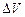 и учитывая, что
и учитывая, что 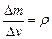 , получим
, получим
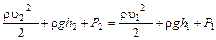 Поскольку S1 и S2 выбраны произвольно
Поскольку S1 и S2 выбраны произвольно
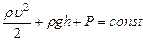 -уравнение Бернулли
-уравнение Бернулли
В идеальной несжимаемой жидкости сумма динамического, гидравлического и статического давлений постоянна на любом поперечном сечении потока.
Для горизонтальной трубки уравнение Бернулли принимает вид 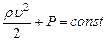
Из уравнения Бернулли и неразрывности следует, что в местах сужения трубопровода скорость течения жидкости возрастает, а давление понижается.
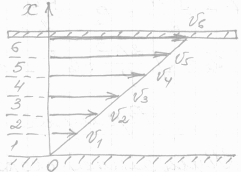
2.При течении реальной жидкости отдельные слои ее воздействуют друг на друга с силами, касательными к слоям. Это явление называется внутренним трением или вязкостью.
Рассмотрим движение жидкости между двумя твердыми пластинками, из которых нижняя неподвижна, а верхняя движется со скоростью 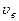 . Слой, прилипший ко дну, неподвижен. Максимальная скорость
. Слой, прилипший ко дну, неподвижен. Максимальная скорость 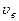 будет у слоя, «прилипшего» к верхней пластинке.
будет у слоя, «прилипшего» к верхней пластинке.
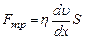 - уравнение Ньютона.
- уравнение Ньютона.
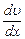 -градиент скорости, S- площадь соприкасающихся слоев жидкости,
-градиент скорости, S- площадь соприкасающихся слоев жидкости, 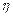 -коэффициент вязкости.
-коэффициент вязкости.
Жидкости, подчиняющиеся уравнению Ньютона, называются ньютоновскими. Жидкости, не подчиняющиеся уравнению Ньютона, называются неньютоновскими. Вязкость ньютоновских жидкостей называют нормальной, неньютоновских - аномальной.
Кровь является неньютоновской жидкостью.
Дата добавления: 2016-05-25; просмотров: 941;
