Энтропия, ее свойства

В термодинамике широко используются величины, кото­рые являются функциями состояния системы. С одной из та.ких функций состояния, внутренней энергией U, мы уже по­знакомились. Еще одной функцией состояния системы, зани­мающей особое место в термодинамике, является энтропия S. Понятие энтропии было введено Клазиусом следующим обра­зом: энтропия S —функция состояния системы, дифференциалом которой является 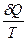, т. е.

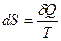, (29.1)

где δQ — элементарное количество теплоты, сообщаемое тер­модинамической системе от термостата с темпера­турой Т при элементарном изменении состояния си­стемы.

Чтобы убедиться в том, что энтропия является функцией состояния системы, нужно показать независимость изменения энтропии ΔS = S₂—S₁ от вида процесса при переходе термо­динамической системы из одного состояния 1 в другое состоя­ние 2. Покажем это на примере идеального газа. Пусть иде­альный газ, образующий замкнутую систему, равновесным образом переходит из состояния 1 в состояние 2, тогда со­гласно (29.1)

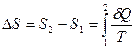. (29.2)

Подставляя в (29.2) из первого начала термодинамики

δQ = dU+δA

и учитывая, что

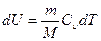и ,

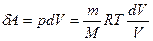получим

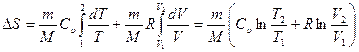, (29.3)

где m — масса газа; М — молярная масса; Т₁, Т₂, V₁, V₂ — температуры и объем газа в состояниях 1 и 2; C_υ — молярная теплоемкость газа при V=const. Из выражения (29.3) видно, что изменение энтропии иде­ального газа при переходе их состояния 1 в 2 не зависит от вида процесса перехода и определяется только параметрами газа V₁ Т₁в состоянии 1 и параметрами V₂, Т₂ в состоянии 2. Если газ участвует в обратимом циклическом процессе, то V₁ = V₂, T₁ = T₂и изменение энтропии газа за цикл равно тождественно нулю

,

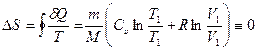что также указывает на то, что энтропия есть функция со­стояния термодинамической системы.

Остановимся на свойствах энтропии. Пусть термодинами­ческая система участвует в циклическом процессе, состоящем из двух участков: 1→2 необратимый процесс и 2→1 обра­тимый. В целом цикл будет необратим, и для него можно записать неравенство Клаузиуса:

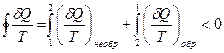. (29.4)

Для обратимого участка цикла имеем

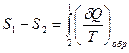. (29.5)

Тогда (29.4) запишется

.

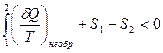откуда

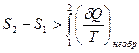. (29.6)

Поскольку на участке 2→1 процесс обратимый, то выраже­ние (29.5) может быть представлено в виде

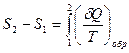. (29.7)

Обобщая формулы (29.6) и (29.7), получим выражение

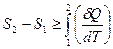, (29.8)

в котором знак равенства берется в случае обратимого про­цесса перехода системы из состояния 1 в состояние 2 и знак больше, если процесс перехода необратимый.

Если рассмотреть изолированную систему, то она не бу­дет обмениваться теплотой с окружающей средой и в фор­муле (29.8) на любой стадии процесса δQ=0. В результате мы получаем, что изменение энтропии будет равно ΔS ≥ 0 или в дифференциальной форме dS ≥ 0, где знак равенства бе­рется для обратимого процесса, и знак больше — в случае необратимого.

Так как реальные процессы необратимы, то на основании (29.8) можно утверждать, что все возможные процессы в теплоизолированной системе ведут к увеличению ее энтропии— принцип возрастания энтропии.

Важным свойством энтропии является ее аддитивность: энтропия системы равна сумме энтропии всех тел (частей), входящих в состав системы:

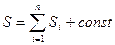, (29.9)

где п — число тел (частей) системы.

Как видно из (29.9), энтропия S известна с точностью до неопределенной постоянной и, следовательно, ее абсолютная величина зависит от выбора начала отсчета, в то время как ее изменение ΔS не зависит от выбора начала отсчета эн­тропии.

Введение понятия энтропии и установление принципа ее возрастания позволяет дать обобщенную формулировку вто­рого начала термодинамики: в замкнутой термодинамической системе возможны лишь такие процессы, которые ведут к возрастанию энтропии.

Далее из (29.8) следует, что для произвольного процесса

δQ ≤ TdS. (29.10)

Если подставить (29.10) в выражение для первого начала термодинамики, получим

TdS ≥ dU+ δA. (29.11)

Последнее неравенство (29.11) объединяет первый и вто­рой законы термодинамики и является ее важнейшим соот­ношением.

2. Термодинамические потенциалы

Термодинамическими потенциалами называют такие функ­ции состояния системы, с помощью которых можно вычис­лить работу, производимую системой в обратимых процессах при заданных условиях, так как термо­динамические потенциалы являются функциями состояния, их изменение зависит только от начального и конечного состояния системы, т. е. они являются полными диф­ференциалами. Конкретный вид термодинамического потен­циала определяется условиями, в которых находится система при переходе из начального 1 в конечное 2 состояние.

При адиабатическом процессе, как это следует из первого начала термодинамики, работа, совершаемая системой, равняется убыли внутренней энергии δA = — dU или A₁-₂ = U₁—U₂. Таким образом:

1) внутренняя энергия системы в адиабатическом процессе играет роль термодинамического потенциала.

2) Важнейшим термодинамическим потенциалом является так называемая энергия Гeльмгoльцa

F=U—TS, (29.12)

термодинамический потенциал при изотермиче­ском процессе. Работа, совершаемая в обратимом изотермическом процессе, равна убыли энергии Гельмгольца или

A₁-₂ = F₁—F₂. (29.13)

Энергия Гельмгольца F меньше внутренней энергии U на величину TS > 0. Произведение абсолютной температуры Т на энтропию S является той частью внутренней энергии си­стемы, которую невозможно в изотермическом обратимом процессе реализовать в виде работы. Эту часть внутренней энергии называют связанной энергией системы. В этом смыс­ле энергия Гельмгольца F является свободной, преобразую­щейся в работу.

3) Наряду со свободной энергией F в термодинамике широко используется термодинамический потенциал, известный как функция Гиббса G:

G = F+ pV = U – TS + pV. (29.14)

Функция Гиббса является изобарно-изотермическим по­тенциалом. Она позволяет рассчитать работу в процессе, при котором сохраняются давление p = const и температура Т = const системы:

δA = — dG или А­_1-2 = G₁ — G₂. (29.15)

В инженерной практике именно этот термодинамический потенциал является наиболее подходящим, так как многие процессы протекают в условиях постоянного давления и тем­пературы.

3. Третье начало термодинамики (теорема Нернста)

Третье начало термодинамики было установлено Нернстом в 1906 г. на основании целого ряда экспериментальных фак­тов, относящихся к исследованиям химического равновесия, и поэтому представляет собой, как и другие законы термоди­намики (нулевое, первое, второе начала), эмпирически уста­новленный принцип.

Третье начало (теорема Нернста) термодинамики форму­лируется следующим образом: энтропия химически однород­ного вещества (тела) конечной плотности при стремлении температуры к абсолютному нулю приближается к предель­ному значению, не зависящему от давления, плотности или фазы вещества.

В силу неопределенности абсолютной величины энтропии можно принять состояние при 0 К за некоторое состояние и считать, что энтропия этого состояния S₀ = 0. Тогда третье начало тремодинамики можно представить в виде

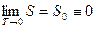(29.16)

и энтропия произвольного состояния определяется однознач­ным образом. Найденную таким образом энтропию называют абсолютной энтропией.

Из третьего начала тремодинамики вытекает ряд следст­вий, которые могут быть проверены на опыте. В частности, из него следует, что теплоемкости вещества при постоянном объеме C_υи при постоянном давлении С_р при Т = 0 должны равняться нулю. Действительно, поскольку 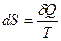и δQ = C_υ(T)dT, имеем

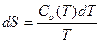, (29.17)

Интегрируя (29.17) в интервале температур от 0 К до Т, получим

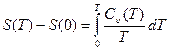. (29.18)

Для того чтобы интеграл (29.18) не расходился на нижнем пределе интегрирования и учитывая, что по третьему началу S(0) = S₀ = 0, теплоемкость C_υ(T)в подынтегральном выра­жении при Т = 0 должна равняться нулю, т. е. C_υ(0)= 0.

Аналогично можно утверждать, что теплоемкость при по­стоянном давлении С_Р(Т)при Т=0 также равна нулю: С_р(0) = 0.

Важнейшим следствием, вытекающим из третьего начала термодинамики, является утверждение о том, что никакими способами нельзя достичь абсолютного нуля температуры (недостижимость абсолютного нуля), т. е. никакую систему невозможно охладить до абсолютного нуля температуры.

В заключение отметим, что третье начало вместе с нуле­вым, первым и вторым началами термодинамики образуют систему основных аксиом, на которых базируется термодина­мика.

4. Статистический смысл энтропии

Физический смысл энтропии S не столь очевиден как, на­пример, физический смысл внутренней энергии U, теплоты Q или работы А. В 1877 г. Людвиг Больцман исходя из основ­ных свойств энтропии (ее возрастание во всех естественных процессах и ее аддитивность) предложил статистическую трактовку энтропии.

Он ввел в теорию теплоты статистические представления, приписав каждому состоянию системы «термодинамическую вероятность» W, которая тем больше, чем более однородным (беспорядочным) по распределению параметров, характери­зующих механическое движение молекул, является это со­стояние.

Возрастание энтропии в этом случае означает, что систе­ма переходит из исходного состояния в другое, термодинами­ческая вероятность которого больше.

Пусть имеется сосуд с перегородкой, разделяющей два газа. Если перегородку убрать, то газы немедленно начнут перемешиваться посредством диффузии, которая является типичным необратимым процессом. Очевидно, что после того, как произошло смешение, маловероятно, чтобы все молекулы каждого сорта газа вернулись в первоначально занимаемые ими части объема сосуда.

Другой пример. Мы можем себе представить как разру­шается старое здание, превращаясь в кучу мусора и кирпи­чей (переход от порядка к беспорядку), но маловероятно, чтобы вдруг эта груда мусора и кирпича превратилась снова в здание (переход от беспорядка к порядку), для этого надо приложить значительные усилия.

Образная трактовка энтропии — это функция, показываю­щая, что в природе все процессы направлены таким образом, чтобы системы переходили в состояния, которые характери­зуются большей степенью беспорядка.

Волна, ударяясь о камни, разбивается на тысячи брызг, но эти брызги не собираются обратно в волну. Таким обра­зом, необратимые процессы продолжаются до тех пор, пока не будет достигнуто наиболее вероятное для этой системы со­стояние, характеризующееся максимумом энтропии.

Принимая во внимание проведенную параллель между тенденцией к переходу в состояния с большей вероятностью (меньшей упорядоченностью) и возрастанием энтропии, Больцман предположил существование функциональной зави­симости S = S(W) между S и W.

Эта функция должна быть монотонно возрастающей. Кро­ме того, оказывается, можно полностью определить ее вид. Пусть имеем систему, состоящую из двух частей А и В, тогда в состоянии равновесия энтропия всей системы будет

S(W) = S_A + S_B. (29.19)

Термодинамическая вероятность W осуществления конеч­ного состояния системы равна произведению термодинами­ческих вероятностей W_A и W_B для отдельных частей системы:

W = W_A ∙ W_B. (29.20)

В соответствии с (29.19) и (29.20) имеем

S(W) = S(W_A ∙ W_B) = S(W_A)+S(W_B). (29.21)

Уравнению (29.21) удовлетворяет логарифмическая функция

S = klnW + const, (29.22)

где k — постоянная Больцмана.

Энтропия — величина физическая и ее численное значе­ние зависит от выбранной системы единиц, а термодинамиче­ская вероятность — величина математическая, ибо она опре­деляется числом способов, которыми может быть реализо­вано данное состояние термодинамической системы.

Коэффициент k обеспечивает гомогенность формулы Больцмана, но именно соотношение между двумя величинами различной природы обуславливает ее научную особенность.

Практическая ценность формулы (29.22) ограничена. Если состояние газа известно (известны Т и р), то нетрудно найти значение S, не используя величину W.

Если же состояния газа неизвестно или известно только частично (кроме массы известен только объем газа), то мы не можем вычислить W и, следовательно, определить вели­чину S. Это не дает нам новых сведений о состоянии газа. Однако формула Больцмана имеет значительный теоретиче­ский интерес — она показывает, что кинетическая теория га­зов позволяет интерпретировать не только давление и тем­пературу газа, но и его энтропию, причем изменение энтропии в одном определенном направлении есть статистическая за­кономерность.

5. Элементы термодинамики необратимых процессов

Разработка термодинамики необратимых процессов, кото­рая давала бы информацию о протекании процессов во вре­мени пока еще далека от завершения. Основные трудности связаны с тем, что до сих пор неизвестно, всегда ли пара­метры, необходимые для описания протекания во времени необратимых процессов, являются функциями только макро­скопических величин.

Однако термодинамике необратимых процессов удалось добиться значительных успехов в решении ряда частных во­просов — изучении процессов, которые представляют поток, устанавливающийся под влиянием постоянно действующего во времени импульса, таких как электрический ток, поток тепла, диффузионный поток и поток вязкой жидкости. Термодинамика необратимых процессов определяет поток (анало­гично тому, как мы это уже делали при рассмотрении явле­ний переноса) как производную по времени некоторой вели­чины. Поток в соответствии с законами переноса Ома, Фурье, Фика и Ньютона пропорционален соответствующей силе (им­пульсу), а коэффициенты пропорциональ-ности (коэффицициенты переноса) должны зависеть от параметров состояния, а не от сил.

Для описания системы в неравновесном состоянии требу­ется вводить большее число параметров, чем для описания системы, находящейся в равновесии.

Так, термически однородная система в состоянии равнове­сия имеет одну температуру, общую для всех частей системы.

Та же система до установления равновесия могла иметь в разных частях различные температуры.

Предположим, что система может быть описана парамет­рами а₁, а₂, .,., а_п.

Термодинамические силы (импульсы) X_i определяются со­отношением

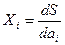, (29.23)

где S — энтропия, а потоки I_i — производными по времени:

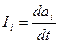. (29.24)

Возникновение энтропии σ, понятие, вводимое в термоди­намике необратимых процессов, определяется соотношением

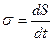. (29.25)

Используя формулы (29.23) и (29.24), получим вместо соот­ношения (29.25) новое:

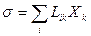. (29.26)

Это уравнение является основным для практических расчетов сил и потоков.

Взаимосвязь между силами и потоками является физиче­ской закономерностью, связывающей измеримые величины.

Теорию процессов переноса, согласующуюся с опытом при медленных потоках, удалось создать, основываясь на про­стейших линейных соотношениях между силами и потоками

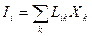. (29.27)

Уравнения такого вида получили наименования феноменоло­гических. Феноменологические коэффициенты L_ik не зависят ни от сил, ни от потоков.

В частном случае, когда имеются только один поток и один импульс, получаем известные феноменологические за­коны.

Закон Ома:

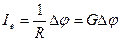, (29.28)

где 1_е — электрический ток; R — сопротивление участка цепи; G — электропроводность; Δφ — разность потенциалов, обуславливающая ток на участке цепи.

Закон Фурье:

I_q = q = – λΔT, (29.29)

где q — поток тепла; λ, — коэффициент теплопроводности; ΔT — разность температур, обуславливающая поток тепла.

Закон Фика:

I_с = —DΔс, (29.30)

где I_с — поток вещества; D — коэффициент концентрационной диффузии; Δс — разность концентраций компонента смеси, обуслав­ливающая поток вещества.

Закон Ньютона:

I_р = —ηΔυ, (29.31)

где I_р — поток импульса; η — коэффициент внутреннего трения; Δυ — разность скоростей, обусловившая поток импульса.

Термодинамика неравновесных процессов позволяет рас­сматривать более общие случаи явлений переноса чем те, что описываются уравнениями (29.28) — (29.31). Она позволяет описать процессы, в которых налагаются друг на друга два или несколько потоков различной физической природы и воз­никают так называемые перекрестные эффекты.

К перекрестным эффектам относятся упоминавшиеся ра­нее явления термодиффузии, диффузионного термоэффекта, а также такие, как термоэлектрический эффект, который нам предстоит еще изучить.