Второе начало термодинамики

Первое начало термодинамики указывает на то, что в любых термодинамических процессах должен выполняться закон сохранения энергии. Однако это начало не дает указаний относительно того, какие процессы невозможны, даже если формально закон сохранения энергии выполняется. Так, из первого начала термодинамики не следует, что не может быть процесса, единственным результатом которого является передача тепла от холодного тела к горячему, если при этом выполняется энергетический баланс: переданная холодным телом теплота равняется увеличению внутренней энергии го­рячего тела плюс работа, совершаемая над окружающей средой. Иными словами, из первого начала термодинамики невозможно определить направление эволюции термодинами­ческой системы, указать на необратимость того или иного процесса. Этот существенный момент нашел свое отражение во втором начале термодинамики, которое установлено эмпи­рическим путем и может быть сформулировано несколькими способами, которые эквивалентны друг другу. Ниже приво­дятся некоторые из формулировок второго начала термо­динамики.

1. Теплота не может самопроизвольно перейти от холод­ного тела к горячему без каких-либо других изменений в си­стеме или, иначе говоря, процесс, при котором единственным результатом является передача тепла от горячего тела к хо­лодному, будет необратимым (принцип Клаузиуса).

2. Невозможен процесс преобразования в работу всего количества теплоты, взятой от тела с однородной температу­рой, без каких-либо других изменений состояния системы или, иначе говоря, процесс, при котором работа переходит в тепло без каких-либо изменений состояния системы, является необ­ратимым (принцип Томсона).

3. Невозможно создать циклически работающую тепловую машину, которая производила бы работу за счет поглощения тепла от одного теплового резервуара, не совершая при этом никаких других изменений состояния системы (принцип невозможности вечного двигателя второго рода).

Все три формулировки второго начала эквивалентны. Чтобы это показать, рассмотрим тепловую машину.

2. Тепловая машина. КПД тепловой машины

Тепловой машиной называют устройство, позволяющее производить работу при циклическом теплообмене между термодинамической системой (рабочим телом) и окружающей средой (термостатом). Примерами тепловой машины могут служить паровые двигатели, двигатели внутреннего сгорания. Рассмотрим с общих позиций принцип действия тепловой ма­шины и ее коэффициент полезного действия.

Как отмечалось ранее, для того чтобы работа за цикл была положительная (А > 0), ветвь расширения цикла в диа­грамме р, V должна иметь более высокое давление, чем ветвь сжатия (см. рис. 28.3, а). Это означает, что при расширении термодинамическая система получает количество теплоты Q₁ от окружающей среды с температурой Т₁(нагреватель), а при сжатии отдает некоторое количество теплоты Q₂ окружа­ющей среде с более низкой температурой Т₂ (холодильник), чем Т₁. Схематично принцип действия тепловой машины пред­ставлен на рис. 29.1.

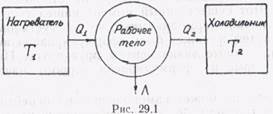
Коэффициент полезного действия тепловой машины η из­меряется отношением работы А, совершаемой за цикл, к ко­личеству теплоты Q₁, полученной в цикле от нагревателя:

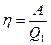. (28.1)

Из первого начала термодинамики для цикла имеем

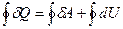. (28.2)

Учитывая, что

, , ,

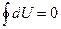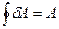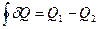из уравнения (28.2) получим

A = Q₁ – Q₂. (28.3)

Используя (28.3), выражение для КПД цикла (28.1) пред­ставится в виде

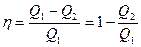. (28.4)

Как видно, тепловые машины работают таким образом, что рабочее вещество расширяется в результате поглощения тепла от резервуара, находящегося при высокой температуре Т₁. Чтобы вернуться к первоначальному состоянию, это ве­щество нужно снова сжать и при этом передать некоторое ко­личество тепла резервуару с более низкой температурой Т₂.

Согласно формулировке 1 второго начала термодинамики, невозможно передать это тепло обратно к высокотемператур­ному резервуару без каких-либо других изменений. Следова­тельно, формулировка 2 второго начала термодинамики спра­ведлива.

Наоборот, в силу формулировки «б» мы не можем извлечь тепло некоторого резервуара, превратить его в работу, а за­тем снова превратить в тепло (трением и т. д.) в резервуаре с более высокой температурой. Таким образом, из формули­ровки 2 вытекает формулировка 1.

Если бы утверждения 1 или 2 не выполнялись, то можно было бы получать тепло от резервуара с постоянной темпе­ратурой и превращать его в работу при помощи циклического процесса. Это не нарушило бы первого закона термодинами­ки, который требует лишь, чтобы для каждого цикла выпол­нялось соотношение Q = А. С практической точки зрения та­кая машина была бы равноценна машине, способной совер­шать работу вечно, ибо в природе существуют источники неограниченных количеств тепла, например мировой океан. Подобную неосуществимую машину называют вечным двига­телем второго рода. Утверждение о невозможности построить вечный двигатель второго рода эквивалентно формулировкам 1 и 2.

3. Цикл Карно, его КПД

Среди различных термодинамических циклов особое место занимает цикл Карно, рассмотренный впервые французским инженером и физиком Сади Карно.

Значение цикла Карно связано с тем, что он позволил проанализировать работу тепловой машины, и, что особенно важно, цикл является в ряде отношений оптимальным и мо­жет служить для анализа второго начала термодинамики.

Циклом Карно называется обратимый круговой процесс, происходящий с термодинамической системой (рабочим те­лом), которая получает от нагревателя тепло при неизменной температуре Т₁ и отдает тепло холодильнику также при неиз­менной температуре Т₂, т. е. изотермически. Изменение тем­пературы рабочего тела от Т₁до Т₂ и обратно от Т₂ до Т₁совершается адиабатически. Таким образом, цикл Карно изображается двумя изотермами и двумя адиабатами (рис. 29.2).

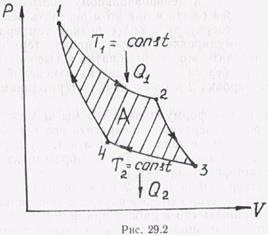
Предположим, что рабочим телом является газ, находя­щийся в цилиндре под поршнем. Пусть первоначально объем газа равен V₁, а температура равна Т₁(точка 1 на рис. 29.2). На участке цикла между точками 1 и 2 газ изотермически расширяется до объема V₂, совершая работу за счет тепла Q₁, получаемого от нагревателя. Чтобы процесс был обрати­мым, необходимо, чтобы температура нагревателя лишь на бесконечно малую величину превосходила температуру газа. Практически Т₁— это температура и нагревателя, и газа. Размеры нагревателя предполагаются настолько большими, что передача тепла газу не повлияет на температуру нагре­вателя. Это обеспечивает изотермический характер процесса.

В точке 2 рабочее вещество теплоизолируется и на участке цикла 2—3 происходит адиабатическое расширение газа. На этом участке работа совершается газом за счет его внутрен­ней энергии. Температура газа падает до температуры холо­дильника Т₂.

На участке цикла 3—4 газ изотермически сжимается. Ра­бота совершается внешними по отношению к газу силами, а газ отдает тепло Q₂ холодильнику. В точке 4 газ теплоизоли­руется, и сжатие продолжается адиабатически. На участке цикла 4—1 внутренняя энергия газа растет и температура по­вышается до температуры нагревателя Т₁. Газ возвращается в первоначальное состояние, совершив работу, равную пло­щади, ограниченной графиком цикла.

Вычислим к.п.д. цикла Карно, считая, что он совершается идеальным газом. Согласно формуле (28.4), к.п.д. любой тепловой машины равен

.

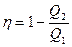Количество тепла Q₁ полученное от нагревателя идеаль­ным газом при температуре Т₁, равно работе, совершенной при изотермическом расширении газа от объема V₁до объема V₂. Поэтому согласно формуле (27.8) имеем

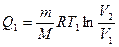. (28.5)

Количество тепла Q₂, отданное холодильнику газом при температуре Т₂, равно работе изотермического сжатия газа от объема Vздо V₄:

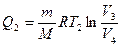. (28.6)

Из уравнения адиабаты (27.27) следует, что для участков цикла Карно 2—3 и 4—1 имеем

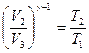и ,

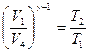откуда

.

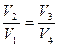Таким образом, отношения объемов в формулах (28.5) и (28.6) для Q₁ и Q₂ оказываются равны между собой. С уче­том этого обстоятельства после подстановки Q₁ и Q₂ в выра­жение для к.п.д. получаем, что для цикла Карно

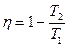. (28.7)

Покажем теперь, что к.п.д. η' любой тепловой машины М′, получающей тепло от нагревателя при температуре Т₁и отдающей тепло холодильнику при температуре Т₂, не может превосходить к.п.д. η_обр обратимой тепловой машины Карно М, работающей между теми же температурными пределами.

Пусть Q₁ и Q₁′ — количества теплоты, полученные машина­ми М и М' за один цикл от нагревателя с температурой Т₁; Q₂и Q₂' — количества теплоты, отданные этими машинами за цикл холодильнику с температурой Т₂(Т₁ > Т₂). Согласно первому началу термодинамики, работы, совершаемые маши­нами М и М' за цикл, будут соответственно равны

А = Q₁ - Q₂ и А' = Q₁′ - Q₂'. (28.8)

Поскольку машина Карно М обратима, заставим ее совер­шать цикл в обратном направлении (в этом случае работа будет отрицательна А < 0), в то время как машина М' совер­шает прямой цикл.

При этом пусть нагреватель Т₁не отдает и не получает тепла (Q₁ = Q₁′). Тогда результат совершения этих двух цик­лов выразится полной работой:

А_полн = А' - А = Q₂ - Q₂', (28.9)

где были использованы соотношения (28.8) при Q₁ = Q₁′.

Если бы А_полн > 0, то это противоречило бы второму на­чалу термодинамики (принцип Томсона), так как тогда бы тепло, отнятое у холодильника, в периодически действующей машине целиком превращалось бы в работу. Поэтому должно быть

А_полн = Q₂ - Q₂' ≤ 0,

откуда

Q₂≤ Q₂'

или

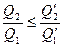(28.10)

при Q₁ = Q₁′.

Используя соотношение (28.10), получаем, что к.п.д. η' тепловой машины М' и к.п.д. η_обр машины М, работающей по обратимому циклу Карно, находятся в соотношении

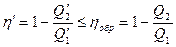. (28.11)

Из (28.11) следует весьма важное для практики заключе­ние: ни в какой тепловой машине не может быть превзойден так называемый термодинамический коэффициент полезного действия 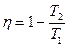обратимой тепловой машины Карно.

В тепловой машине, использующей необратимый цикл, к.п.д. всегда меньше, чем в машине, работающей по обрати­мому циклу в том же температурном пределе от Т₁до Т₂. Это связано с потерями энергии, обусловленными трением, теплопроводностью и другими необратимыми явлениями.

4. Неравенство Клаузиуса

Поскольку к.п.д. тепловой машины, работающей по обратимому циклу, 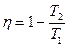, из выражения (28.11) вытекает в общем случае следующее соотношение:

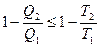, (28.12)

в котором знак равенства берется в случае обратимого цикла и знак неравенства — для необратимого цикла.

Путем элементарных алгебраических преобразований из (28.12) получаем

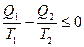. (28.13)

Если Q₂, теплоту, отдаваемую термодинамической систе­мой окружающей среде, рассматривать как отрицательное количество теплоты, получаемое системой от внешней среды, то (28.13) представляется в виде

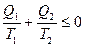. (28.14)

Отношение количества тепла Q, получаемого системой от какого-либо тела, к абсолютной температуре Т тела, при которой происходит теплопередача, 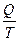называется приведенной теплотой. Эту терминологию предложил Клаузиус. Используя терминологию Клаузиуса, соотношение (28.14) означает сле­дующее: если термодинамическая система совершает цикл, в ходе которого она вступает в теплообмен с двумя тепло­выми резервуарами (телами), температуры которых посто­янны (T₁ = const, T₂ = const), то сумма приведенных количеств теплоты равна нулю, если цикл обратим, и меньше нуля, если цикл необратим.

Если система в ходе цикла вступает в тепловой контакт с N телами, то выполняется соотношение

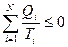. (28.15)

В выражении (28.15) предполагается, что температура каждого из N тел, обменивающихся теплом с системой, в ходе цикла не изменяется (Т_i = const). Если это не так, т. е. тем­пература i-го тела T_i при передаче тепла Q_i системе меняется, то можно каждый из процессов теплопередачи разбить на ряд элементарных процессов, чтобы передачу тепла δQ в каждом из них можно было считать происходящей при постоянной температуре Т. Тогда в ходе цикла будем иметь:

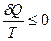, (28.16)

т. е. сумма элементарных приведенных количеств тепла, по­лучаемых термодинамической системой за цикл, равна нулю, если цикл обратимый, и меньше нуля, если цикл необратимый.

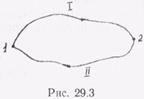Выражения (28.15) или (28.16) известны в термодина­мике как неравенство Клаузиуса. Сумму приведенных количеств тепла можно рассматривать не только для циклов, но и для любого нециклического процесса. Для обратимых процессов эта сумма обладает следующим свой­ством: она не зависит от формы пути (от способа), по которому термодинамическая система переходит от начального состояния к конечному. Действительно, представим себе некоторый обратимый цикл, который разобьем на два участка (пути) I (1—2) и II (2—1) (рис. 29.3).

На основании неравенства Клаузиуса (28.16) для такого цикла имеем

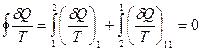. (28.17)

Поскольку цикл обратимый, то изменение направления перехода на участке II (2→1) на противоположное II (1→2) приведет к изменению знака 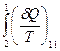на противоположный, т. е.

.

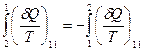С учетом этого обстоятельства из (28.17) вытекает, что

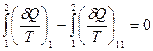или .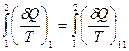

Таким образом, сумма элементарных количеств теплоты, получаемых системой при обратимом переходе из состояния 1 в другое состояние 2, не зависит от формы пути, по которому совершается переход, и зависит, следовательно, только от на­чального (1) и конечного (2) состояния.