Внутренняя энергия системы. Работа и теплота

Первое начало термодинамики.

Первое начало термодинамики является частным случаем общего закона сохранения энергии. Содержание первого на­чала может быть сформулировано следующим образом: при переходе системы из начального состояния 1 в конечное состояние 2, получаемая системой от окружающей среды сумма теплоты Q, энергии переноса массы Z (Z — энергия, которая передается системе при переносе массы вещества из окру­жающей среды в систему) и совершаемой средой работы А', определяется только состояниями 1 и 2; эта сумма не зависит от того, каким способом осуществляется переход из 1 в 2.

Это означает, что существует такая величина U, характе­ризующая внутреннее состояние системы, разность значений которой в состояниях 1 и 2 определяется соотношением

U₂ — U₂ = Q + Z + A'. (27.1)

Величина U представляет собой внутреннюю энергию си­стемы. Внутренняя энергия — это энергия, заключенная в си­стеме. При этом обычно не учитывается кинетическая энергия системы в целом и потенциальная энергия системы во внеш­нем поле (хотя в некоторых случаях потенциальную энергию можно рассматривать как часть внутренней энергии). При микроскопическом рассмотрении внутренняя энергия равна сумме кинетической энергии теплового движения молекул, энергии взаимодействия между ними, а также внутриатомной и ядерной энергии. Однако термодинамика не затрагивает вопрос о природе внутренней энергии. Из первого начала термодинамики вытекает, что внутренняя энергия U является функцией состояния системы и, следовательно, не зависит от способа перехода системы из одного состояния в другое.

Величина внутренней энергии определяется с точностью до некоторой аддитивной постоянной. Эту постоянную можно зафиксировать, выбрав внутреннюю энергию исходного со­стояния системы за нулевую точку отсчета внутренней энер­гии.

Соотношение (27.1) представляет выражение наиболее общей формулировки первого начала термодинамики.

Существуют частные формулировки. Рассмотрим некото­рые из них. Если система закрытая, то Z = 0, так как систе­ма не обменивается веществом с окружающей средой. В этом случае соотношение (27.1) представится как

U₂ — U₁ = Q+A'. (27.2)

Работа А', совершаемая средой над системой, может быть заменена взятой с обратным знаком работой А, которую си­стема совершает над средой (А' =—А). С учетом этого обстоятельства из (27.2) вытекает, что

Q = A + U₂ — U₁, (27.3)

Следовательно, согласно (27.3), первое начало термодина­мики для закрытой системы можно сформулировать следую­щим образом: теплота, подводимая к закрытой системе, идет на изменение внутренней энергии и на работу, совершаемую системой над окружающей средой. При сообщении системе малого (элементарного) количества теплоты δQ первое на­чало термодинамики (27.3) записывается в дифференциаль­ной форме:

δQ = δA + dU. (27.4)

В (27.4) различные обозначения изменений δQ, δА и dU подчеркивают то обстоятельство, что U, в отличие от Q и А, является функцией состояния системы, для которой при лю­бом циклическом процессе полное изменение внутренней энергии тождественно равно нулю ( 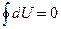) и, следова­тельно, dU представляет полный дифференциал. Работа А и теплота Q не являются функциями состояния системы, они 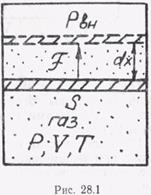зависят от условий перехода термодинамической системы изодного состояния в другое. Их изменения зависят от пути пере­хода, и они называются вариа­циями. Покажем это на примере закрытой системы, представляю­щей собой газ, находящийся в цилиндре с подвижным поршнем площадью S (рис. 28.1). В об­щем случае работа, произведен­ная системой, состоит в смеще­нии границы ее поверхности S, следовательно, в изменении ее объема V и преодолении при этом некоторого давления р_вн внешней среды (рис. 28.1). В случае квазистатического процесса в любой момент времени дав­ление газа р будет равно внешнему давлению р_вн (р = р_вн). С учетом этого обстоятельства работа, совершаемая силой F = pS при смещении границы поверхности на малый отре­зок dx, будет равна

δА= Fdx = р∙Sdx = pdV, (27.5)

где dV = S∙dx— элементарное изменение объема газа.

При расширении газа dV > 0 и δА > 0; в случае сжатия dV < 0 и δА < 0, так как давление газа всегда положитель­но. Формула (27.5) дает выражение для элементарной рабо­ты. Для того чтобы найти работу А, совершаемую системой (газом) при переходе из состояния 1 в состояние 2, необхо­димо проинтегрировать (27.5):

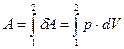. (27.6)

Пусть газ расширяется от объема V₁до V₂при неизмен­ном давлении р = const (рис. 28.2, а). Тогда из (27.6) сле­дует, что работа, совершаемая газом, будет равна

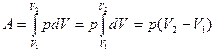. (27.7)

Vi Vi

На рис. 28.2, а эта работа соответствует заштрихованной площади фигуры, ограниченной графиком изобарного про­цесса и ординатами начального и конечного состояния газа (V₁ и V₂).

Расширение газа от объема V₁ до V₂ может происходить также при неизменной температуре Т = const (рис. 28.2, б), т. е. изотермически. В этом случае работа, совершаемая га­зом, будет иной:

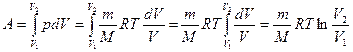. (27.8)

При выводе формулы (27.8) было использовано уравне­ние состояния идеального газа, из которого давление газа .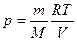

В диаграмме р, V, как и в случае изобарного процесса, работа А представляется заштрихованной площадью фигуры, ограниченной графиком изотермического процесса (pV = const) и ординатами начального и конечного состояния газа V₁ до V₂.

Если расширение газа протекает адиабатически, т. е. без теплообмена с окружающей средней (δQ = 0), то, как следует из первого начала термодинамики (27.4), δА = —dU и

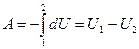, (27.9)

где U₁ и U₂ — внутренняя энергия термодинамической систе­мы в начальном и конечном состоянии соот­ветственно.

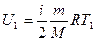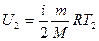Учитывая, что для идеального газа и , формула (27.9) запишется

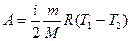. (27.10)

Из выражений (27.7), (27.8) и (27.10) видно, что работа при расширении идеального газа зависит от характера про­цесса. Она различна для изобарного, изотермического и адиабатического процессов. Для изохорного процесса (V = const, dV = 0) работа равна нулю. При циклическом про­цессе работа, совершаемая за цикл, может быть рассчитана аналитически по формуле

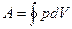(27.11)

или графически, как площадь заштрихованной фигуры, огра­ниченной циклом, в диаграмме состояний термодинамической системы (рис. 28.3).

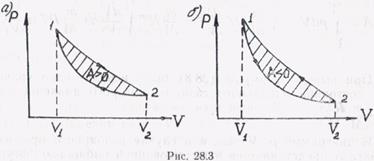
Причем в случае прямого направления протекания цикла (ветвь расширения 1—2 лежит выше ветви сжатия 2—1) работа положительна (рис. 28.3, а), при обратном направлении цикла (ветвь расширения 1—2 лежит ниже ветви сжа­тия 2—1) работа отрицательна (рис. 28.3, б).

2. Теплоемкость. Теплоемкость идеального газа

Подводимое к системе элементарное количество теплоты δQ в общем случае можно записать в форме

δQ = CdT, (27.12)

где dT — элементарное увеличение температуры; С — теплоемкость системы (тела).

Как видно из (27.12), теплоемкость системы (тела) чис­ленно равняется количеству тепла, которое требуется сооб­щить системе (телу), чтобы увеличить его температуру на один градус

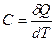. (27.13)

Теплоемкость единицы массы системы (тела) называется удельной теплоемкостью одного моля вещества — молярной теплоемкостью.

Теплоемкость термодинамической системы зависит от ее массы, химического состава и от вида процесса, в ходе кото­рого к системе подводится теплота.

Получим молярные теплоемкости идеального газа для изохорного C_υ, изобарического С_р, адиабатического С_а и изо­термического С_тпроцессов. Для этого воспользуемся выраже­нием (27.13) и первым началом термодинамики (27.4).

Для изохорного процесса, как следует из первого начала термодинамики, δQ = dU и, следовательно, теплоемкость

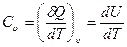. (27.14)

Подставляя в (27.14) для 1 моля идеального газа

,

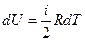получим

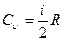. (27.15)

При изобарном процессе

δQ = dU + pdV

и теплоемкость будет

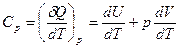. (27.16)

Подставив в (27.16)

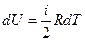, и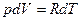

имеем

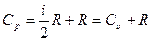. (27.17)

Адиабатический процесс протекает без теплообмена термо­динамической системы с окружающей средой (δQ = 0). Сле­довательно, теплоемкость системы в таком процессе отсут­ствует:

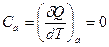. (27.18)

В случае изотермического процесса, когда Т = const и dT = 0, теплоемкость системы бесконечная величина:

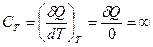, (27.19)

Таким образом, молярная теплоемкость идеального газа (27.15), (27.17), (27.18), (27.19) в различных процессах раз­лична, поэтому и теплота, подводимая к идеальному газу для его нагревания из состояния с температурой Т₁ до состоя­ния Т₂, также будет разная.

Действительно, если в указанном интервале температуры от Т₁ до Т₂ теплоемкость не изменяется, то из (27.12) по­лучаем

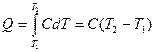. (27.20)

Подставляя в (27.20) вместо С значения из (27.15), (27.17), имеем:

изохорный процесс

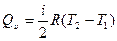. (27.21)

изобарный процесс

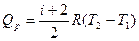. (27.22)

3. Уравнение адиабаты для идеального газа

Как уже отмечалось, термодинамический процесс, при ко­тором система не получает и не отдает тепло (δQ = 0), на­зывается адиабатическим.

Из первого начала термодинамики следует, что для этого процесса

δА = —dU, (27.23)

т. е. работа совершается за счет изменения внутренней энер­гии системы.

Адиабатический процесс осуществляется в теплоизолиро­ванной системе. Требования к теплоизоляции определяются временем протекания процесса. Если процесс протекает до­статочно быстро, теплообмен не успевает произойти, и про­цесс будет адиабатическим; если же процесс протекает мед­ленно, требования к теплоизоляции становятся более жест­кими. В дальнейшем предположим, что адиабатический про­цесс должен протекать настолько медленно, чтобы состояние системы можно было считать равновесным в любой момент времени. Рассмотрим в качестве закрытой адиабатической системы один моль идеального газа.

Бесконечно малая работа при квазистатическом процессе изменения объема на величину dV равна δА = pdV, а бес­конечно малое изменение внутренней энергии одного моля газа .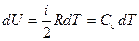

Поэтому при адиабатическом процессе на основании (27.23) имеем

pdV = — C_υdT. (27.24)

Полученное соотношение показывает, что при адиабатиче­ском расширении температура газа падает, а при адиабати­ческом сжатии температура газа растет. Это объясняется тем, что при расширении газ совершает работу за счет уменьше­ния своей внутренней энергии, а при сжатии работа внешних сил идет на увеличение внутренней энергии газа.

Воспользовавшись уравнением состояния идеального газа, перепишем уравнение (27.24) в виде

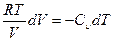. (27.25)

Используя связь между С_р и C_υ (27.17), имеем

R = С_р — C_υ. (27.26)

Подставив (27.26) в (27.25) и обозначив 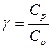, получим

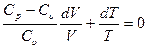или .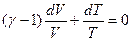

Считая γпостоянной величиной, запишем последнее соот­ношение в виде

,

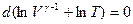откуда

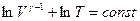. (27.27)

или окончательно

.

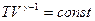Величина γназывается показателем адиабаты и для газов 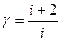, где i — число степеней свободы молекул. Для одноатомных газов 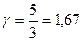, для двухатомных 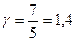, для многоатомных .

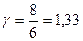Формула (27.27) означает, что между температурой Т₁и объемом V₁газа в начальном состоянии и температурой Т₂ и объемом V₂ газа в конечном состоянии, возникшем в ре­зультате адиабатического процесса, существует соотношение

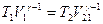или .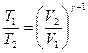

Преобразуем полученное соотношение, воспользовавшись уравнением состояния идеального газа. Из уравнения состоя­ния следует, что

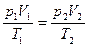или ,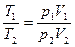

поэтому для адиабатического процесса получаем

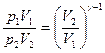или .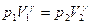

Таким образом, при адиабатическом процессе с идеальным газом

pV^γ = const. (27.28)

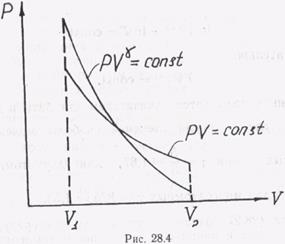
Выражения (27.27) и (27.28) называют уравнением ади­абаты. График адиабатического процесса (адиабаты) изобра­жен на рис. 28.4. Для сравнения на этом же рисунке дан график изотермического процесса, для которого pV = const. При адиабатическом расширении давление убывает быстрее, чем при изотермическом, так как γ > 1.