Способы описания состояния вещества

Существуют три способа описания состояния вещества:

1) молекулярно-кинетический, основанный на рассмотре­нии движения и взаимодействия частиц (атомов и молекул), из которых состоит исследуемое вещество;

2) статистический, основанный на рассмотрении всей со­вокупности частиц вещества, образующих систему; свойства частиц определяются как средние для всей совокупности на основе функции распределения;

3) термодинамический, в котором не учитывается микро­скопическое строение вещества, а его физические свойства рассматриваются через функции состояния в зависимости от термодинамических параметров (давления, температуры, мас­сы вещества, объема системы) с помощью ряда аксиом (на­чала термодинамики).

В молекулярно-кинетическом способе рассматривают пару взаимодействующих частиц вещества. Определяют полную энергию 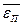взаимодействия в зависимости от расстояния r между частицами как сумму кинетической энергии 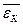и по­тенциальной U(r) в расчете на частицу:

.(15.1)

Кинетическая энергия определяется тепловым хаотическим движением частиц и выступает как мера разупорядоченности структуры вещества.

Для определения величины U(r) необходимо выбрать одну из моделей взаимодействия пары частиц (молекул или ато­мов) вещества. Выбор модели базируется на основе значе­ний параметров состояния, фазового состояния, строения мо­лекул или атомов изучаемого вещества, достаточной точности результатов расчета и расчетных возможностей.

Наиболее распространенные физические модели потенци­альных функций взаимодействия для пары частиц (молекул, атомов) приведены в прил. I.

Величина потенциальной энергии парного взаимодействия рассматривается как мера упорядоченности и ограниченности перемещения частиц вещества друг относительно друга.

Сопоставляя величины 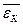и U(r), можно судить о фазо­вых состояниях вещества:

1) если 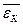> |U(r)|, то вещество находится в газовом со­стоянии;

2) если 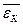< |U(r)|, то вещество пребывает в твердом со­стоянии;

3) если 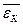~ U(r), то вещество — жидкость.

Для твердого состояния тепловое движение частиц веще­ства ограничено колебаниями и вращениями, а поступатель­ное движение отсутствует. Расстояние между частицами ве­щества в твердом состоянии постоянно; оно называется по­стоянной кристаллической решетки.

Для жидкого состояния при низких температурах преиму­щественными являются локализованные колебания, как у твердых тел. Скачкообразные поступательные перемещения отдельных частиц маловероятны. При высоких температурах в жидкостях доля частиц, которые могут совершать поступа­тельные скачки на расстояни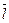е (где 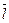— средняя длина про­бега), растет с ростом температуры Т, и при Т>Т_К поступа­тельная форма движения превалирует над колебательной.

Для описания твердого состояния хороши модели потен­циальных функций прямоугольной потенциальной ямы, гар­монического осциллятора и модели Морзе (Ленарда—Джон­са), для газообразного — модель идеального газа Сазерленда или потенциала Ленарда—Джонса (прил. II). Жидкости при низких температурах (близких к температуре замерзания) принято рассматривать как квазитвердое состояние с соответствующими модельными представлениями, а при высоких — как квазигазовое.

Энергетические характеристики вещества при молекулярно-кинетическом описании получают суммированием полной энергии (15.1) в расчете на одну частицу по числу частиц п, образующих систему:

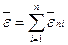. (15.2)

Эта величина используется для расчета теплоемкостей, по­верхностного натяжения и т. д. Явления переноса (диффу­зия, вязкость, теплопроводность и т. д.) описываются, основываясь на особенностях движения частиц вещества в зави­симости от фазового состояния, для каждой конкретной модели взаимодействия и значений параметров состояния (давления р и температуры Т).

Статистический способ описания является наиболее об­щим и универсальным способом описания состояния веще­ства. Он соединяет в себе как макроскопический, так и мик­роскопический (молекулярно-кинетический) подход. Основ­ным понятием при статистическом подходе является функция распределения числа частиц по некоторому физическому па­раметру (чаще всего по энергиям, импульсам, либо скоро­стям движения). Функция распределения характеризует для частиц, образующих систему, вероятность того, что интере­сующий нас параметр имеет величину, лежащую в некотором определенном интервале значений, или характеризует долю от общего числа частиц, для которых значение интересую­щего нас параметра лежит в некотором определенном интервале.

Зная вид функции распределения, можно методами мате­матической статистики определить средние значения физиче­ских величин, характеризующих вещество в целом.