Работа дифференциала, блокировка
Дифференциал служит для распределения потока мощности между ведущими мостами или колесами в определенной пропорции, обеспечивая независимое вращение ведомых звеньев с различными угловыми скоростями (на повороте, по неровной дороге, при различном давлении воздуха в шинах или разном износе протектора, разной степени загрузки ведущих колес и т.д.)
| Корпус |
| Полуосевые шестерни |
| Палец |
| Сателлит |
| ω |
| F = 0 |
| Ось с зазором |
| Механическая модель сателлита |
Рис. 21.1. Схема работы симметричного дифференциала
Момент от ведомой шестерни ГП передается жестко закрепленному с ней корпусу дифференциала. От него момент переходит на встроенный в корпус палец сателлита. С пальца – на сателлит, который может свободно вращаться на пальце. Сателлит представляет собой шестерню (коническую в данном случае) и находится в зацеплении одновременно с двумя полуосевыми шестернями, на зубья которых передает силу от пальца.
Поскольку сателлит может свободно вращаться на пальце (см. правую часть рис. 21.1.), то сила его давления на одну полуосевую шестерню не может отличаться от силы на другую. Именно поэтому моменты на обоих колесах будут равны, независимо от угловых скоростей колес (разные угловые скорости колес легко обеспечиваются сателлитом его свободным вращением вокруг своей оси).
Отмеченное положительное свойство дифференциала в определенных дорожных условиях вызывает большие проблемы. Например: если одно колесо (предположим верхнее на рис. 21.1.) находится в воздухе и поворачивается свободно, то к нему нельзя приложить усилие со стороны сателлита (колесо не оказывает реакции). Сателлит, легко вращаясь на пальце, обкатывает полуосевую шестерню другого, стоящего на земле колеса, и не может нагрузить ее. В таком случае на обоих колесах из-за работы дифференциала сила тяги будет равна нулю.
Подобный эффект произойдет, если одно из колес находится на поверхности с низким сцеплением (грязь или лед). Другому колесу, стоящему на асфальте сателлит дифференциала будет сообщать точно такой же момент, как первому, т.к. силы по обе стороны сателлита могут быть только одинаковы.
Таким образом, общая сила тяги ведущих колес при работающем симметричном дифференциале определяется колесом, находящимся в худших условиях сцепления с дорогой.
Если сателлиту не позволить вращаться на пальце вокруг своей оси (заблокировать), то он сможет передавать усилие даже одной своей стороной на одно ведущее колесо (например, когда другое колесо повисло в воздухе). В случае заблокированного дифференциала кинематические и силовые взаимодействия будут такими, как если правое и левое ведущие колеса соединены одной жесткой осью. Проходимость автомобиля значительно повышается из-за полного использования сцепления с дорогой каждым ведущим колесом независимо от другого.
Принудительно заблокировать дифференциал (исключить возможность проворота сателлита) можно, используя, например такую конструкцию (Рис. 21.2.):
| Блокирующая муфта |
| Привод включения муфты |
| Зубчатые венцы |
| ω |
| F >> 0 |
| Ось заблокирована от поворота |
Рис. 21.2. Схема принудительной блокировки дифференциала
В этой конструкции блокирующая муфта установлена на полуоси с помощью шлицев. Она имеет зубчатый венец, которым может соединиться с зубчатым венцом, закрепленным на ведомой шестерни ГП. При зацеплении зубчатых венцов с помощью привода исключается возможность вращения сателлита вокруг своей оси (см. Рис. 21.2. справа снизу и сверху) – принудительное блокирование дифференциала.
Существуют принципиально другие конструкции, повышающие проходимость автомобиля. В них провороту сателлита на пальце препятствует трение. Такой дифференциал называются дифференциалом повышенного трения (самоблокирующийся). Пока трение не позволяет провернуться сателлиту, дифференциал вообще заблокирован, как в предыдущем случае. Например, если одно колесо в воздухе, то сателлит давит на полуосевую шестерню другого колеса силой трения, мешающей ему проворачиваться на пальце. Момент трения продолжает действовать и далее, после того, как сателлит начал вращаться вокруг пальца. Момент трения всегда передается сателлитом отстающему колесу (стоящему неподвижно или вращающемуся медленнее другого, забегающего), потому что именно надавливая на его полуосевую шестерню сателлит преодолевает трение, начиная проворачиваться. По этой причине, в случае буксования одного колеса на другое (отстающее) идет момент больший, чем на буксующее (забегающее) на величину момента трения в дифференциале.
Конструктивно получить трение, мешающее повороту сателлита вокруг пальца можно, например, так:
| Корпус дифференциала |
| Фрикционные прокладки |
| ω |
| МТ |
| F > 0 |
| Ось поворачивается с трудом |
Рис. 21.3. Схема работы дифференциала повышенного трения
В обычных дифференциалах (не повышенного трения) также имеется некоторый момент трения, обусловленный касанием сателлита и полуосевых шестерен корпуса дифференциала.
Все выше сказанное относится и к межосевому дифференциалу с той разницей, что вместо ведущих колес у него ведущие мосты.
21.2. Классификация дифференциала
1. По расположению в трансмиссии.
1) Межколесные (рассмотрен выше).
2) Межосевой:
2. По кинематике.
1) Симметричный (рассмотрены выше).
2) Несимметричный:
Этот дифференциал распределяет на передние ведущие колеса одну часть момента, а назадние – две, соответственно количеству ведущих мостов.
3. По способу распределения момента между ведомыми звеньями.
1) Неблокируемые.
2) Самоблокирующиеся (повышенного трения).
3) С принудительной блокировкой.
4.По конструкции.
1) Шестеренчатые конические (из набора конических шестерен, как показано выше на схемах и чертежах).
2) Шестеренчатые цилиндрические (на рисунке – межосевой несимметричный):
| Ведомая шестерня раздаточной коробки |
| Сателлит |
| К переднему мосту |
| К задним двум мостам |
3) Червячные.
4) Кулачковые.
5) С муфтами свободного хода.
21.3. Кинематические и силовые аспекты работы дифференциала
В общем случае движения по множеству причин одно из колес имеет угловую скорость отличную от другого. Допустим, что нижнее (на рис. 21.4.) колесо отстаёт (либо вращается медленнее другого, либо стоит на месте), а верхнее – забегает.
| ωзаб, Мзаб |
| ωд, Мд |
| ωот, Мот |
Рис. 21.4. Схема распределения моментов и скоростей вращения полуосей
Для симметричного дифференциала зависимость, связывающая угловые скорости колес ωот, ωзаб и корпуса дифференциала ωд выглядит так:
(ωот + ωзаб) / 2 = ωд
А в идеальном случае, когда скорости колес равны, они вращаются со скоростью корпуса дифференциала:
ωот = ωзаб = ωд.
Момент с корпуса дифференциала распределяется по колесам так:
Мот + Мзаб = Мд.
В то же время, о чем говорилось выше, на отстающее колесо действует такой же момент, как на забегающее и еще добавляется момент трения в дифференциале - Мт:
Мот = Мзаб + Мт.
В идеальном случае момент распределяется между колесами поровну.
Величина момента трения в дифференциале говорит о степени его заблокированности. Определяется эта величина коэффициентом блокировки:
Кб = Мот / Мзаб.
Поскольку по условиям сцепления: Мот = Fк от∙ rк = φот∙ Gк ∙ rк,
Мзаб = Fк заб ∙ rк = φзаб∙ Gк ∙ rк , то получим выражение для коэффициента блокировки:
Кб =φот /φзаб. Здесь rr – радиус качения колеса, Gк – вес, приходящийся на ведущее колесо (принят одинаковым на оба колеса), φ - коэффициент сцепления между колесом и дорогой.
Если под одним колесом асфальт (φ = 0,8), а под другим – лед (φ = 0,1), то коэффициент блокировки потребуется: Кб = 0,8 / 0,1 = 8, чтобы колеса полностью использовали сцепление с дорогой. Применив записанные выше выражения можно определить, какой требуется для такого случая момент трения в дифференциале:
Кб = Мот / Мзаб = (Мзаб + Мт) / Мзаб = 1 + Мт / Мзаб =
= 1 + Мт / φзаб∙ Gк ∙ rк.
Подставив сюда Кб = 8 и φзаб = 0,1 получим выражение для момента трения: Мт = 0,7∙ Gк∙ rк. Это очень высокое внутреннее трение и его может обеспечить только дифференциал специальной конструкции (самоблокирующийся), например, червячный.
Несмотря на лучшую проходимость автомобиля с дифференциалом повышенного трения, имеются существенные недостатки:
- из-за потерь на трение падает КПД трансмиссии;
- увеличивается расход топлива;
- ухудшается управляемость и устойчивость автомобиля на твердой дороге;
- увеличивается износ шин.
Обычно у большинства дорожных автомобилей Кб = 2…2,5;
у кулачкового (повышенного трения) – 3…4;
у червячного – 6…12;
у принудительно заблокированного - Кб = ∞.
21.4. Основы расчета дифференциала
rср
r1
ωд
FД
FС
Ось сателлитов
l2
l1
d
Рис. 21.5. Схема для расчета дифференциала на прочность
В этом дифференциале два сателлита расположенных на одной оси.
На каждый сателлит от корпуса дифференциала через ось действует сила:
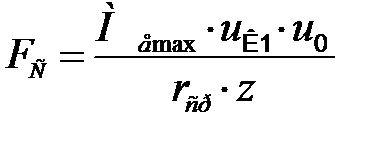 , (21.1)
, (21.1)
где Меmax – максимальный момент двигателя, uК1 – передаточное число КП первой передачи, uo – передаточное число главной передачи, rср – средний радиус приложения силы к сателлиту, r1 – радиус приложения силы в корпусе, Z – число сателлитов.
От этой силы ось под сателлитом испытывает напряжение смятия:
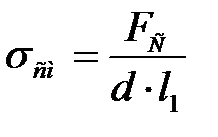 , (21.2)
, (21.2)
d – диаметр оси, допускаемое напряжение 
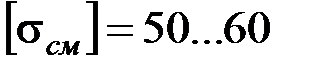 МПа.
МПа.
Напряжение среза пальца по основанию сателлита:
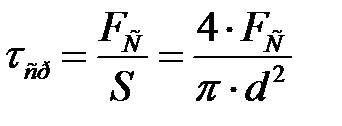 , (21.3)
, (21.3)
S – площадь среза, допускаемое напряжение 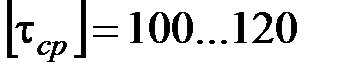 МПа.
МПа.
В корпусе дифференциала на ось действует сила смятия:
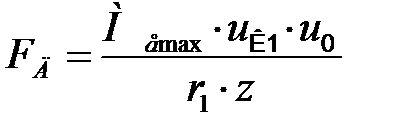 . (21.4)
. (21.4)
Под действием этой силы ось в корпусе испытывает напряжение смятия:
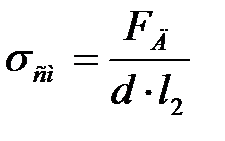 , (21.5)
, (21.5)
допускаемое напряжение 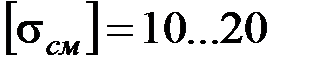 МПа.
МПа.
§22 ПОЛУОСИ
Полуоси предназначены для передачи потока мощности от дифференциала на ведущие колеса. Полуоси могут частично или полностью воспринимать силы и моменты, действующие на колеса.
22.1. Классификация полуосей
1. По условиям нагружения.
1) Полностью нагруженная:
Сейчас такая конструкция не применяется, поскольку поломка полуоси между подшипником и корпусом дифференциала приводит к разрушению балки моста и главной передачи.
2) Полуразгруженная:
Такая конструкция применяется в легковых автомобилях классической компоновки.
3) На 3/4 разгруженная полуось:
Конструкция применялась раньше на грузовых автомобилях. Теперь не применяется.
4) Полностью разгруженная полуось:
Применяется на современных грузовых автомобилях.
2. По конструктивным особенностям (по назначению).
1) Безшарнирные.
2) Шарнирные (у переднеприводных).
3. По способу связи с ведущими колесами.
1) Фланцевые.
2) Безфланцевые.
22.2. Основы расчета полуосей
Разгруженные полуоси рассчитываются по напряжению кручения:
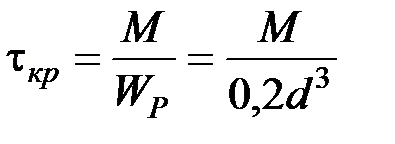 , (22.1)
, (22.1)
где: 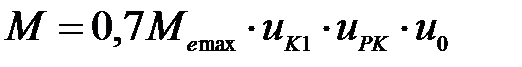 .
.
Коэффициент 0,7 перед моментом двигателя говорит о том, что из-за трения в дифференциале на отстающее колесо может передаваться больше половины момента (70% в данном случае).
Для расчета других полуосей нужно кроме крутящего момента учитывать все силовые факторы, действующие на колесо.
| МК |
| FК |
| FТ |
| GK или GКД |
| RY |
| rК |
| МТ |
Рис. 22.1. Силовые факторы, действующие на колесо
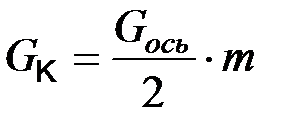 – величина статической нагрузки на колесо, m - коэффициент перераспределения нагрузки по осям при разгоне и торможении (1,1…1,4 – большие значения у легковых автомобилей).
– величина статической нагрузки на колесо, m - коэффициент перераспределения нагрузки по осям при разгоне и торможении (1,1…1,4 – большие значения у легковых автомобилей).
GКД = GК∙КД – динамическая нагрузка на колесо при движении по неровной дороге. КД = 2 для дорожных автомобилей, для автомобилей повышенной проходимости – 3…4.
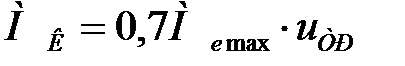 - момент на колесе, он же момент на полуоси - повторение формулы из начала раздела,
- момент на колесе, он же момент на полуоси - повторение формулы из начала раздела,
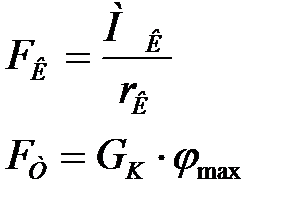
FК, FТ – тяговая и тормозная силы на колесе, rк – радиус качения колеса принимается равным радиусу качения в ведомом режиме, φmax – коэффициент сцепления колеса с дорогой.
RY – боковая сила:
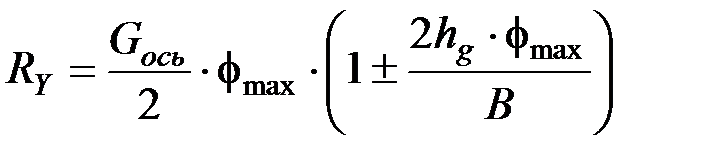 ,
,
здесь hg – высота центра тяжести автомобиля, В – колея автомобиля.
Поскольку эти силовые факторы действуют не одновременно, а в определенном сочетании, расчет полуосей, а также балок мостов производится по четырем расчетным режимам поочередно. В результате выбирается наиболее напряженный режим из возможных:
1. Движение с максимальной тяговой силой.
Учитываются силовые факторы: GK, МК, FК.
2. Движение с предельным торможением:
GK, FТ, МТ – если тормозной момент через полуось не передается (с колеса через тормозной механизм воспринимается балкой), то он и не учитывается в этом режиме.
3. Движение с боковым заносом:
GK, RY.
4. Движение по неровной дороге с высокой скоростью:
GКД.
Пример расчета полуоси (полуразгруженной)
| RY |
| GК |
| a |
| FТ |
| FК |
| rК |
| МК |
1. По первому расчетному режиму:
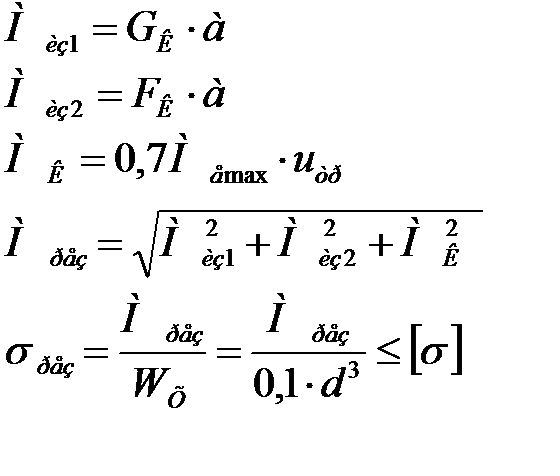
2. По второму расчетному режиму:
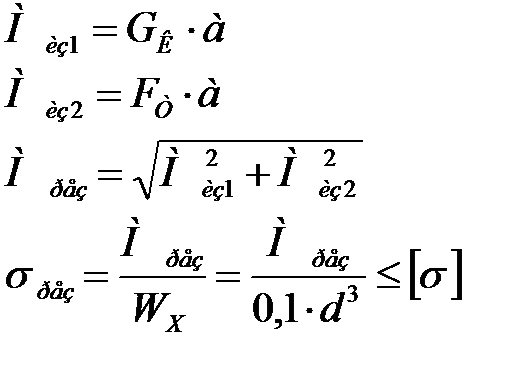
3. По третьему расчетному режиму:
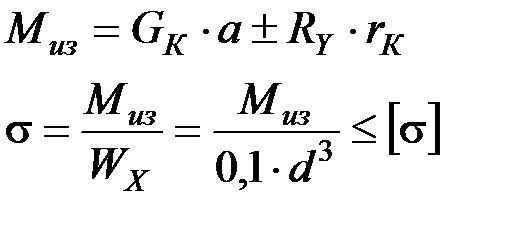
4. По четвертому расчетному режиму:
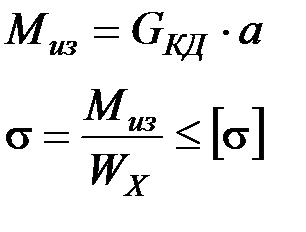
Материал полуосей – сталь 40ХН, закалка с нормализацией.
§23 БАЛКИ МОСТОВ
Балка служит для жесткой связи между собой ведущих или управляемых колес автомобиля, а также для передачи силовых факторов на подвеску.
23.1. Классификация балок
1. По выполняемым функциям (назначению) бывают балки мостов:
1) Поддерживающих.
2) Ведущих.
3) Управляемых.
2. По технологии изготовления:
1) Кованные.
2) Литые.
3) Комбинированные.
3. По особенностям конструкции:
1) Неразъемные.
2) Разъемные.
23.2. Основы расчета балок
Наиболее нагруженным сечением является зона крепления упругого элемента подвески. Расчет производится на сложнонапряженное состояние по четырем расчетным режимам, как у полуосей:
1. Движение с максимальной тяговой силой.
GK, МК.
2. Движение с предельным торможением:
GK, FТ, МТ
3. Движение с боковым заносом:
GK, RY.
4. Движение по неровной дороге с высокой скоростью:
GКД.
При расчете балки ведущих мостов необходимо учитывать тип полуосей. У балок разгруженных (Рис. 23.1.) и на 3/4 разгруженных полуосей расчет изгибных напряжений в сечении 1-1 от сил, действующих в плоскости качения колеса производится на плече а. Определяются изгибающие моменты в вертикальной и горизонтальной плоскостях и закручивающий момент от тормозной силы. Затем определяется результирующий момент Миз (в отличии от полуосей, в первом расчетном режиме крутящего момента не будет, а во втором режиме появляется тормозной момент, который передается на балку от тормозного щита). Результирующий момент делится на момент сопротивления изгибу WX и так определяется напряжение изгиба.
| GК |
| а |
| FТ |
| FК |
| rК |
| МТ |
| RY |
Рис. 23.1. Расчетная схема балки ведущего моста
Крутящий момент тоже воспринимается балкой, но он расположен по другую сторону опасного сечения (в данном случае) или вообще не достигает места крепления упругого элемента (с ним работает отдельный узел направляющего элемента подвески – реактивные штанги).
При расчете балок управляемых мостов (Рис. 23.2.) надо учитывать наличие шарнира поворотного устройства колеса (например – шкворень в данном случае) и изогнутость балки в вертикальной плоскости:
| rК |
| FК или FТ |
| GК |
| f |
| а |
| в |
| с |
| RY |
Рис. 23. 2. Расчетная схема балки управляемого моста
Расчет изгибающего напряжения в горизонтальной плоскости от тяговых (если мост еще и ведущий) или тормозных сил производится с переносом действия этих сил на ось шарнира (т.е. силы будут действовать на плече в). Это происходит потому, что на плече а до шкворня момент от указанных сил уравновешивается рулевой трапецией. В ней возникают силы растяжения и сжатия, мало влияющие на саму балку.
При расчете балки на кручение в опасном сечении необходимо уменьшить плечо rК на величину с(изгиб балки под двигателем (Рис. 23.2.):
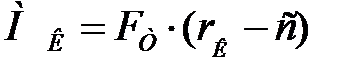
Расчет цапфы поворотного кулака производится в опасном сечении на плече f и только при действии боковой силы (Рис. 23.2.):
Миз = GК ∙f + RY∙rК.
Шкворень (стержень шарнира поворотного кулака, как показано на рис. 23.2.) рассчитывается на изгиб, срез и смятие по нижней, наиболее нагруженной части, входящей в нижнюю проушину поворотной цапфы.
§24 ПОДВЕСКА АВТОМОБИЛЯ
Подвеска служит для снижения динамических нагрузок на автомобиль при его движении по неровной дороге.
Дата добавления: 2016-05-25; просмотров: 1135;
