Расчет по прочности железобетонных элементов при действии поперечных сил
Общие положения
8.1.31 Расчет по прочности железобетонных элементов при действии поперечных сил производят на основе модели наклонных сечений.
При расчете по модели наклонных сечений должны быть обеспечены прочность элемента по полосе между наклонными сечениями и наклонному сечению на действие поперечных сил, а также прочность по наклонному сечению на действие момента.
Прочность по наклонной полосе характеризуется максимальным значением поперечной силы, которое может быть воспринято наклонной полосой, находящейся под воздействием сжимающих усилий вдоль полосы и растягивающих усилий от поперечной арматуры, пересекающей наклонную полосу. При этом прочность бетона определяют по сопротивлению бетона осевому сжатию с учетом влияния сложного напряженного состояния в наклонной полосе.
Расчет по наклонному сечению на действие поперечных сил производят на основе уравнения равновесия внешних и внутренних поперечных сил, действующих в наклонном сечении с длиной проекции С на продольную ось элемента. Внутренние поперечные силы включают поперечную силу, воспринимаемую бетоном в наклонном сечении, и поперечную силу, воспринимаемую пересекающей наклонное сечение поперечной арматурой. При этом поперечные силы, воспринимаемые бетоном и поперечной арматурой, определяют по сопротивлениям бетона и поперечной арматуры растяжению с учетом длины проекции С наклонного сечения.
Расчет по наклонному сечению на действие момента производят на основе уравнения равновесия моментов от внешних и внутренних сил, действующих в наклонном сечении с длиной проекции С на продольную ось элемента. Моменты от внутренних сил включают момент, воспринимаемый пересекающей наклонное сечение продольной растянутой арматурой, и момент, воспринимаемый пересекающей наклонное сечение поперечной арматурой. При этом моменты, воспринимаемые продольной и поперечной арматурой, определяют по сопротивлениям продольной и поперечной арматуры растяжению с учетом длины проекции С наклонного сечения.
Расчет железобетонных элементов по полосе между наклонными сечениями
8.1.32 Расчет изгибаемых железобетонных элементов по бетонной полосе между наклонными сечениями производят из условия
Q £ φb1 × Rb × b × h0, (8.55)
где Q - поперечная сила в нормальном сечении элемента;
φb1 - коэффициент, принимаемый равным 0,3.
Расчет железобетонных элементов по наклонным сечениям на действие поперечных сил
8.1.33 Расчет изгибаемых элементов по наклонному сечению (рисунок 8.6) производят из условия:
Q £ Qb + Qsw, (8.56)
где Q - поперечная сила в наклонном сечении с длиной проекции С на продольную ось элемента, определяемая от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения; при этом учитывают наиболее опасное загружение в пределах наклонного сечения;
Qb - поперечная сила, воспринимаемая бетоном в наклонном сечении;
Qsw - поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении.
Поперечную силу Qb определяют по формуле
0138S10-03623
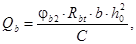 (8.57)
(8.57)
но принимают не более 2,5Rbt × b × h0и не менее 0,5Rbt × b × h0;
φb2 - коэффициент, принимаемый равным 1,5.
0138S10-03623
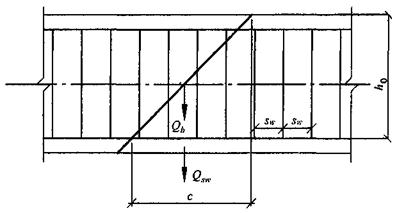
Рисунок 8.6 - Схема усилий при расчете железобетонных элементов по наклонному сечению на действие поперечных сил
Усилие Qsw для поперечной арматуры, нормальной к продольной оси элемента, определяют по формуле
Qsw = φsw × qsw × C, (8.58)
где φsw - коэффициент, принимаемый равным 0,75;
qsw - усилие в поперечной арматуре на единицу длины элемента, равное
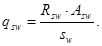 (8.59)
(8.59)
Расчет производят для ряда расположенных по длине элемента наклонных сечений при наиболее опасной длине проекции наклонного сечения С. При этом длину проекции С в формуле (8.58) принимают не менее 1,0h0 и не более 2,0 h0.
Допускается производить расчет наклонных сечений, не рассматривая наклонные сечения при определении поперечной силы от внешней нагрузки, из условия
Q1 £ Qb1 + Qsw,1, (8.60)
где Q1- поперечная сила в нормальном сечении от внешней нагрузки;
Qb1 = 0,5Rbt × b × h0;(8.61)
Qsw,1 = qsw × h0. (8.62)
При расположении нормального сечения, в котором учитывают поперечную силу Q1,вблизи опоры на расстоянии а менее 2,5 h0 расчет из условия (8.60) производят умножая значения Qb1,определяемые по формуле (8.61), на коэффициент, равный 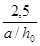 , но принимают значение Qb1не более 2,5 Rbt × b × h0.
, но принимают значение Qb1не более 2,5 Rbt × b × h0.
При расположении нормального сечения, в котором учитывают поперечную силу Q1,на расстоянии а менее h0 расчет из условия (8.60) производят, умножая значение Qsw,1,определяемое по формуле (8.62), на коэффициент, равный a/h0.
Поперечную арматуру учитывают в расчете, если соблюдается условие
qsw ³ 0,25Rbt × b.
Можно учитывать поперечную арматуру и при невыполнении этого условия, если в условии (8.56) принимать
Qb = 4φb2 × h02 × qsw/C.
Шаг поперечной арматуры, учитываемой в расчете, sw/h0 должен быть не больше значения 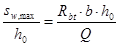 .
.
При отсутствии поперечной арматуры или нарушении указанных выше требований, а также приведенных в 10.3 конструктивных требований расчет производят из условий (8.56) или (8.60), принимая усилия Qsw или Qsw,1 равными нулю.
Поперечная арматура должна отвечать конструктивным требованиям, приведенным в 10.3.
8.1.34 Влияние сжимающих и растягивающих напряжений при расчете по полосе между наклонными сечениями и по наклонным сечениям следует учитывать с помощью коэффициента φn, на который умножают правую часть условий (8.55), (8.56) или (8.60).
Значения коэффициента φn принимаются равными:

| при 0 £ σcp £ 0,25Rb; |
| 1,25 | при 0,25Rb £ σср £ 0,75Rb; |
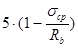
| при 0,75Rb £ σср £ Rb; |
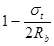
| при 0 £ σt £ 2Rbt, |
где σср - среднее сжимающее напряжение в бетоне от воздействия продольных сил, принимаемое положительным. Величину σср принимают как среднее напряжение в сечении элемента с учетом арматуры.
σt - среднее растягивающее напряжение в бетоне от воздействия продольных сил, принимаемое положительным.
Величины σcp и σt принимают как средние напряжения в сечениях элементов. Допускается величины σcp и σt определять без учета арматуры при содержании продольной арматуры не более 3 %.
Расчет железобетонных элементов по наклонным сечениям на действие моментов
8.1.35 Расчет железобетонных элементов по наклонным сечениям на действие моментов (рисунок 8.7) производят из условия
M £ Ms + Msw, (8.63)
где М - момент в наклонном сечении с длиной проекции С на продольную ось элемента, определяемый от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения, относительно конца наклонного сечения (точка 0), противоположного концу, у которого располагается проверяемая продольная арматура, испытывающая растяжение от момента в наклонном сечении; при этом учитывают наиболее опасное загружение в пределах наклонного сечения;
Мs - момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения (точка 0);
Msw - момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения (точка 0).
Момент Ms определяют по формуле
Ms = Ns × zs,(8.64)
где Ns - усилие в продольной растянутой арматуре, принимаемое равным Rs × As,а в зоне анкеровки определяемое согласно 10.3.21 - 10.3.28;
zs - плечо внутренней пары сил; допускается принимать zs = 0,9 h0.
Момент Msw для поперечной арматуры, нормальной к продольной оси элемента, определяют по формуле
Msw = 0,5 × Qsw × C, (8.65)
где Qsw - усилие в поперечной арматуре, принимаемое равным qsw × С;
qsw - определяют по формуле (8.59), а С принимают в пределах от 1,0 h0 до 2,0 h0.
Расчет производят для наклонных сечений, расположенных по длине элемента на его концевых участках и в местах обрыва продольной арматуры, при наиболее опасной длине проекции наклонного сечения С, принимаемой в указанных выше пределах.
Допускается производить расчет наклонных сечений, принимая в условии (8.63) момент М в наклонном сечении при длине проекции С на продольную ось элемента, равной 2,0 h0,а момент Msw - равным 0,5qsw × h02.
0138S10-03623
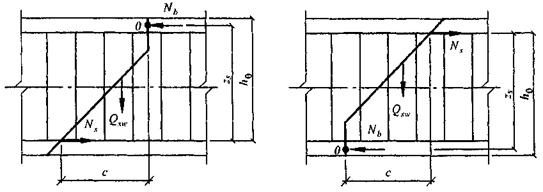
Рисунок 8.7 - Схема усилий при расчете железобетонных элементов по наклонному сечению на действие моментов
Дата добавления: 2016-05-25; просмотров: 3008;
