Векторная диаграмма

Для наглядности синусоидальные величины изображают векторами, вращающимися против часовой стрелки со скоростью, равной угловой частоте ω этих синусоид. Так как эти векторы изображают синусоиды в начальный момент времени (t=0), то они неподвижны. Длина вектора определяет амплитуду синусоиды, а угол поворота вектора против часовой стрелки относительно положительного направления оси абсцисс равен начальной фазе синусоиды. Таким образом, совокупность длины вектора в масштабе и угла поворота вектора относительно оси абсцисс есть векторная диаграмма переменной синусоидальной величины. Т.е. эта векторная диаграмма содержит все значения, характеризующие синусоидальную величину, - амплитуду, угловую частоту и начальную фазу.

Векторные диаграммы синусоидальных величин можно складывать и вычитать как обычные вектора. Они строятся по аналитическому выражению переменной величины:

e1=Em1*Sin (ωt+56); e2=Em2*Sin (ωt-30); e3=Em3*Sin ωt.

Векторные диаграммы можно также строить по графическому представлению переменных синусоидальных величин (см. ниже).

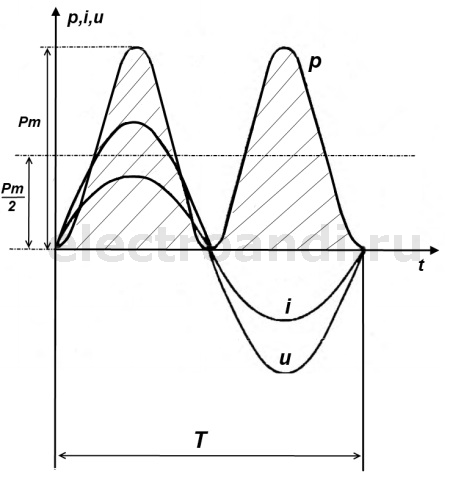
38. Цепь переменного тока с индуктивностью. Её векторная диаграмма.

Под действием синусоидального напряжения в цепи с индуктивной катушкой без ферромагнитного сердечника проходит синусоидальный ток 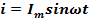.В результате этого вокруг катушки возникает переменное магнитное поле и в катушке наводится ЭДС самоиндукции. При R = 0 напряжение источника целиком идет на уравновешивание этой ЭДС; следовательно, u = -e_L. Так как e_L = - 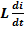, то

,

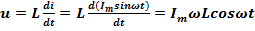или

,

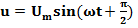где

.

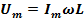Таким образом, по фазовому углу напряжение на катушке индуктивности опережает переменный ток на четверть периода.