Турбулентное течение неньютоновских жидкостей
Турбулентное течение неньютоновских жидкостей более сложно в изучении, чем турбулентное течение ньютоновской вязкой жидкости, поскольку турбулизация ламинарного течения во многих случаях приводит к изменению внутренней структуры самой жидкости. Так, например, для застывающей или высоко парафинистой нефти, транспортируемой по трубопроводу в турбулентном режиме, жесткая пространственная структура, образрвавшаяся в период, когда нефть покоилась или двигалась в ламинарном режиме, разрушается, поэтому свойства возникающей среды изменяются. В ряде случаев они оказываются близкими к свойствам ньютоновской вязкой жидкости с некоторой эквивалентной вязкостью или неньютоновской степенной жидкости с определенным индексом и консистентностью. Вопрос о том, к какому классу относятся подобные жидкости, решается отдельно в каждом конкретном случае.
Вязкопластичная жидкость. Для расчета коэффициента гидравлического сопротивления  в турбулентном течении вязкопластичных жидкостей в гидравлически гладких трубах А.Г.Потапов предложил изменить универсальный закон сопротивления (см. формулу (8.49) гл. 8) и представил этот закон в следующем виде:
в турбулентном течении вязкопластичных жидкостей в гидравлически гладких трубах А.Г.Потапов предложил изменить универсальный закон сопротивления (см. формулу (8.49) гл. 8) и представил этот закон в следующем виде:
 , (11.19)
, (11.19)
где 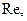
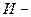 числа Рейнольдса и Ильюшина (11.9), соответственно.
числа Рейнольдса и Ильюшина (11.9), соответственно.
Уравнение (11.19) - это трансцендентное алгебраическое уравнение, выражающее зависимость 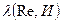 в неявном виде. Уравнение можно разрешить методом последовательных приближений - задавая значения чисел
в неявном виде. Уравнение можно разрешить методом последовательных приближений - задавая значения чисел 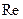 и
и 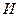 и, используя метод итераций, можно вычислить искомое значение
и, используя метод итераций, можно вычислить искомое значение  .
.
Степенная жидкость. Для турбулентного течения степенной жидкости в области гидравлически гладких труб видоизмененный универсальный закон сопротивления получили Д.Додж и А.Мецнер:
 , (11.20)
, (11.20)
где  индекс (показатель степени в реологическом законе (11.2) [ ]. Уравнение (11.20) так же, как и (11.19) представляет собой трансцендентное алгебраическое уравнение, выражающее коэффициент
индекс (показатель степени в реологическом законе (11.2) [ ]. Уравнение (11.20) так же, как и (11.19) представляет собой трансцендентное алгебраическое уравнение, выражающее коэффициент  гидравлического сопротивления через число
гидравлического сопротивления через число 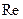 Рейнольдса и индекс
Рейнольдса и индекс 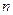 течения в неявном виде. Для вычисления
течения в неявном виде. Для вычисления  по известным значениям
по известным значениям 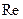 и
и 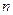 необходимо разрешить уравнение (11.20), что можно сделать методом последовательных приближений.
необходимо разрешить уравнение (11.20), что можно сделать методом последовательных приближений.
Для более удобного вычисления коэффициента  гидравлического сопротивления Н.А.Романова предложила явные зависимости
гидравлического сопротивления Н.А.Романова предложила явные зависимости 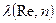 , являющиеся аппроксимацией решений уравнения (11.20) [ ]:
, являющиеся аппроксимацией решений уравнения (11.20) [ ]:
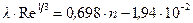 , если
, если  ;
;
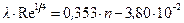 , если
, если 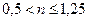 ; (11.21)
; (11.21)
 , если
, если 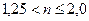 .
.
В формулах (11.20) и (11.21) обобщенное число Рейнольдса определяется как 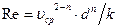 (
( 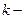 кинематическая консистентность).
кинематическая консистентность).
Как правило, переход от ламинарного течения к турбулентному происходит при значениях обобщенного числа Рейнольдса 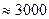 .
.
Дата добавления: 2016-05-16; просмотров: 1162;
