Коэффициент гидравлического сопротивления. Если ввести в рассмотрение среднюю по сечению скорость течения жидкости, число Рейнольдса и так называемое число Ильюшина согласно равенствам
Если ввести в рассмотрение среднюю по сечению скорость 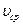 течения жидкости, число Рейнольдса
течения жидкости, число Рейнольдса 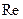 и так называемое число Ильюшина
и так называемое число Ильюшина 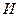 согласно равенствам
согласно равенствам
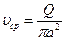 , и
, и 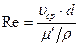 ,
, 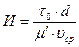 (11.9)
(11.9)
где 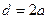 , то выражение (11.8) можно записать в привычной форме закона Дарси-Вейсбаха
, то выражение (11.8) можно записать в привычной форме закона Дарси-Вейсбаха
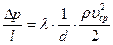 ,
,
где 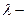 коэффициент гидравлического сопротивления. Если дополнительно учесть, что
коэффициент гидравлического сопротивления. Если дополнительно учесть, что
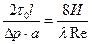 ,
,
то для коэффициента  получим выражение:
получим выражение:
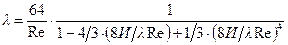 . (11.10)
. (11.10)
Если 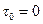 , то
, то 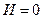 и, следовательно,
и, следовательно, 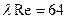 , т.е. формула (11.10) переходит в известную формулу (7.28) Стокса для ламинарного течения вязкой жидкости. В общем случае произведение
, т.е. формула (11.10) переходит в известную формулу (7.28) Стокса для ламинарного течения вязкой жидкости. В общем случае произведение 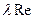 зависит от числа Ильюшина. Для того, чтобы найти это произведение, необходимо разрешить уравнение (11.10) относительно
зависит от числа Ильюшина. Для того, чтобы найти это произведение, необходимо разрешить уравнение (11.10) относительно 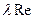 для каждого значения параметра И [ ].
для каждого значения параметра И [ ].
Пример 1. По трубе с диаметром 100 мм и длиной 300 м требуется перекачивать глинистый раствор, необходимый для буровых работ. Известно, что глинистый раствор представляет собой неньютоновскую вязкопластичную жидкость, обладающую предельным напряжением сдвига 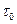 = 15 Па, вязкостью
= 15 Па, вязкостью 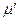 = 0,012
= 0,012 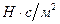 и плотностью
и плотностью 
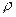 =1250 кг/м3. Определить расход раствора, если движущий перепад давлений равен 5 ат.
=1250 кг/м3. Определить расход раствора, если движущий перепад давлений равен 5 ат.
Решение. Сначала проверим, достаточен ли перепад давления в 5 ат. для возникновения течения жидкости в трубе. Для этого проверим выполнение необходимого условия (11.7); имеем:
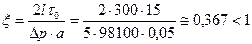 ,
,
следовательно, перепад давлений 5 ат. достаточен для возникновения течения в трубе с данными радиусом и длиной.
Для вычисления расхода воспользуемся формулой (11.8):
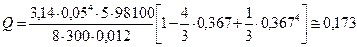
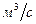
или 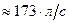 .
.
Дата добавления: 2016-05-16; просмотров: 1165;
