Распределение скорости по сечению трубы

Распределение скорости течения вязкопластичной жидкости по сечению трубы можно получить, если использовать формулы (7.11) гл.7 и (11.4). Имеем:

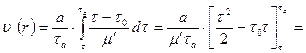
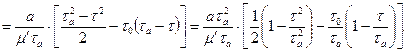
Учитывая, что

,

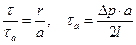после несложных преобразований получаем:

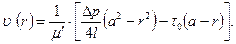
где ради упрощения введено обозначение .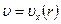

Обозначим посредством 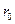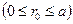радиус жесткого ядра, на поверхности которого касательное напряжение 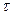равно минимально возможному значению 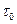, тогда

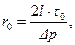
и распределение скоростей 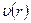жидкости имеет вид:

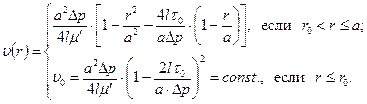(11.6)

Следовательно, эпюра скоростей состоит частью из поверхности параболоида вращения от стенки трубы до цилиндрической поверхности радиуса 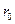(ядра течения), частью из плоской площадки, перпендикулярной оси трубы (рис.11.5). В центральной части трубы вязкопластичная жидкость движется как твердый стержень.

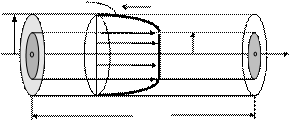
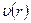
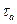
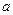
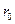
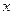
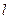
Рис. 11.5. Схема течения вязкопластичной жидкости

Если в распределении (11.6) положить 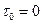, т.е. считать, что предельное напряжение сдвига в жидкости отсутствует, а сама она является ньютоновской вязкой жидкостью ( 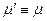), то придем к ранее полученному распределению скоростей (7.16), в котором жесткое ядро исчезает.

Необходимое условие для начала течения жидкости Бингама-Шведова в круглой трубе. Поскольку в вязкопластичной жидкости существует предельное напряжение 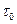сдвига, то ее течение в круглой трубе может начаться лтшь тогда, когда кассательное напряжение 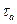станет больше 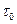. Отсюда получаем необходимое условие для начала течения этой жидкости в трубе:

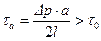, т.е. 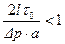. (11.7)

Распределение (11.6) скорости жидкости справедливо только в том случае, если выпролнено условие (11.7).