Характеристики индивидуального объема

Рассмотрим положение объема, состоящего из одних и тех же частиц, в два последовательных момента времени t и 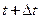(рис.4.2). По определению полной производной можно записать

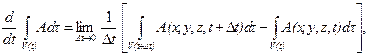(4.7)

где 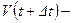объем пространства, занимаемый рассматриваемыми частицами в момент времени .

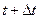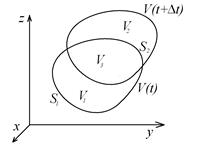
Рис. 4.2. Положение индивидуального объема жидкости в два последующие момента времени

Пусть 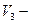объем общей част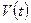и и 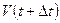, 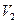—объем части пространства вновь занятого частицами подвижного объема ( 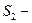часть поверхности 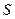, через которую частицы выходят), 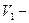объем части пространства, освобожденного частицами, подвижного объема ( 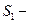часть поверхности S, через которую частицы входят). Тогда каждый из интегралов по объемам 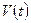и 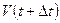в равенстве (4.7) можно разбить на две части

,

.

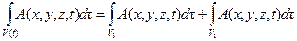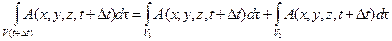Подставляя это разбиение в формулу (4.7), получаем:

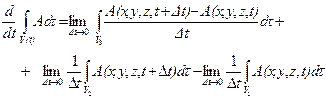. (4.8)

Первое слагаемое в правой части (4.8) равно интегралу от частной производной по времени величины :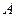

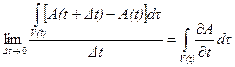. (4.9)

Второе и третье слагаемые можно преобразовать в интегралы по поверхности, ограничивающей подвижный объем.

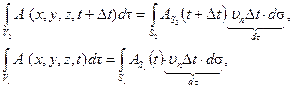(4.10)

где 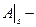значения параметра 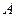в точках поверхности 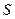. Здесь было использовано представление элементарного объема 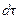в бесконечно тонком слое вокруг поверхносте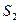й и 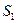виде объема цилиндра с площадью основания 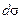(элемент поверхности) и образующей 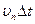( 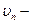проекция вектора скорости частиц на нормаль к поверхности), (рис. 4.3).

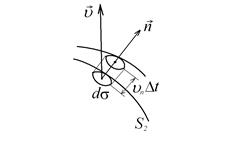
Рис. 4.3.Вычисление элементарного объема 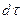в точках

поверхности индивидуального объема

Подставляя (4.10) в (4.8) и переходя к пределу при 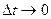, получаем:

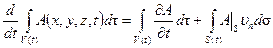. (4.11)

Здесь учтено, что для непрерывной функции имеет место равенство .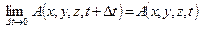

Контрольная поверхность

Физический смысл формулы (4.11) особенно ясно выявляется при использовании понятия контрольная поверхность. Контрольная поверхность - это неподвижная в пространстве поверхность, с которой в некоторый момент времени совпадает поверхность рассматриваемого подвижного объема. Поскольку контрольная поверхность и ограничиваемый ею объем части пространства неподвижны, то интеграл

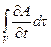
представляет собой скорость изменения величины А в данном объеме пространства, а поверхностный интеграл

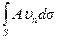
дает скорость изменения параметра А за счет его «потока» через контрольную поверхность.

Таким образом, полная производная по времени от некоторой интегральной характеристики подвижного объема равна частной производной по времени от этой характеристики, вычисленной для неподвижного контрольного объема, с которым подвижный объем совпадает в данный момент, плюс поток количества А через поверхность контрольного объема.

Если течение жидкости - установившееся, то во всех точках пространства

,

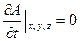следовательно, для установившегося движения имеет место соотношение

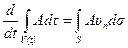. (4.12)

Это равенство означает, что при установившемся течении жидкости изменение любой интегральной характеристики подвижного объема равно потоку этой характеристики через контрольную поверхность.

Отметим, что основные теоремы механики системы материальных точек можно применять к любому подвижному объему среды, поэтому в формуле (4.10) объем и поверхность, его ограничивающая, произвольны.