Показатели размера и интенсивности вариации
Для характеристики размера вариации в статистике применяются абсолютные показатели вариации: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение и дисперсия.
Размах вариации (размах колебаний) представляет собой разность между максимальным и минимальными значениями признака в совокупности:
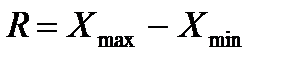
Для группировок с открытыми первым и последним интервалами, когда неизвестны реальные минимальное и максимальное значения признака совокупности, расчет размаха вариации некорректен.
Размах вариации зависит от величины только крайних значений признаков. Более точно характеризуют вариацию признака показатели, основанные на учете колеблемости всех значений признака, — среднее линейное отклонение (d) и среднее квадратическое отклонение (σ).
Для сгруппированных данных они рассчитываются по формулам:
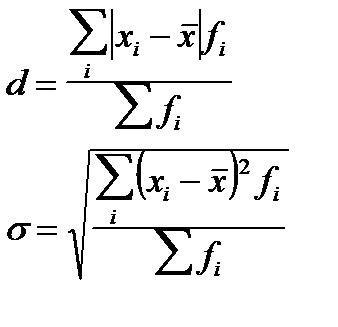 ,
,
где  — значение признака в i-й группе (для интервальных вариационных рядов — середина i-го интервала);
— значение признака в i-й группе (для интервальных вариационных рядов — середина i-го интервала);
 — средняя величина признака в совокупности;
— средняя величина признака в совокупности;
 — частота (частость) i-го интервала.
— частота (частость) i-го интервала.
Квадрат среднего квадратического отклонения называется дисперсией( 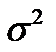 ):
):
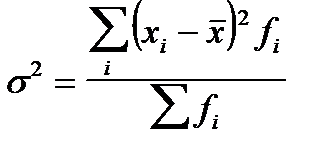
Рассчитать дисперсию можно также по преобразованной формуле:

где 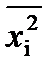 — средний квадрат значений признака в совокупности:
— средний квадрат значений признака в совокупности:
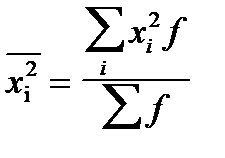 ;
;
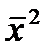 — квадрат среднего значения признака в совокупности.
— квадрат среднего значения признака в совокупности.
При расчете дисперсии по этой формуле исключается дополнительная процедура расчета отклонений индивидуальных значений признака от его средней величины, за счет этого уменьшается ошибка, связанная с округлением значений промежуточных вычислений.
Размах вариации, среднее линейное отклонение и среднее квадратическое отклонение являются величинами именованными, то есть имеют ту же единицу измерения, что и изучаемый признак. Дисперсия единицы измерения не имеет.
Соотношение 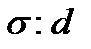 зависит от наличия в совокупности резких отклонений и может служить индикатором «засоренности» совокупности нетипичными, выделяющимися из основной массы единицами. Для нормального распределения это соотношение равно 1,25.
зависит от наличия в совокупности резких отклонений и может служить индикатором «засоренности» совокупности нетипичными, выделяющимися из основной массы единицами. Для нормального распределения это соотношение равно 1,25.
Для оценки интенсивности вариации, а также для сравнения ее величины в разных совокупностях или по разным признакам используют относительные показатели вариации, которые рассчитываются как отношение абсолютных показателей вариации к средней величине признака: относительный размах вариации (коэффициент осцилляции), относительное линейное отклонение и др.
Наиболее часто на практике применяют коэффициент вариации ( 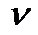 ), который представляет собой относительное квадратическое отклонение:
), который представляет собой относительное квадратическое отклонение:

По величине коэффициента вариации можно судить об интенсивности вариации признака, а следовательно, и об однородности состава изучаемой совокупности. Чем больше величина коэффициента вариации, тем больше разброс значений признака вокруг средней, тем больше неоднородность совокупности. Существует шкала определения степени однородности совокупности в зависимости от значений коэффициента вариации.
| Коэффициент вариации (%) | Степень однородности совокупности |
| до 30 | однородная |
| 30–60 | средняя |
| 60 и более | неоднородная |
Отметим, что приведенная выше шкала оценки однородности совокупности весьма условна. Вопрос о степени интенсивности вариации должен решаться для каждого изучаемого признака индивидуально исходя из сравнения наблюдаемой вариации с некоторой ее обычной интенсивностью, принимаемой за норму.
Вопросы для самоконтроля
1. Что называется вариацией?
2. Какие этапы предполагает статистический анализ вариаций?
3. Какие основные элементы можно выделить в составе любого вариационного ряда?
4. Чем отличаются частости от частот?
5. Что такое гистограмма?
6. Как строится полигон распределения для графического изображения интервального вариационного ряда?
- Как соотносятся между собой среднее значение признака, медиана и мода:
а) в симметричном распределении;
б) при левосторонней асимметрии;
в) при правосторонней асимметрии?
Дата добавления: 2016-05-16; просмотров: 1885;
